直接看 SAM 怎麼 update parameters, 論文的 figure 2: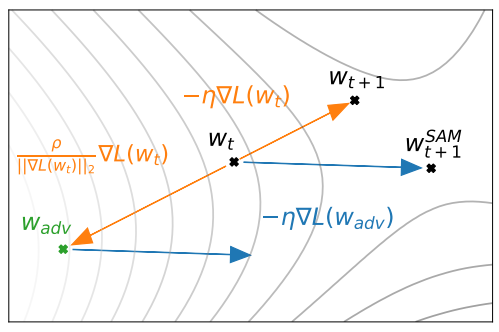 目前的 weight $w_t$ 的 gradient step 為 $-\eta\nabla L(w_t)$, update 後會跑到 $w_{t+1}$.
目前的 weight $w_t$ 的 gradient step 為 $-\eta\nabla L(w_t)$, update 後會跑到 $w_{t+1}$.
SAM 會考慮 $w_t$ locally loss 最大的那個位置 ($w_{adv}$), 用該位置的 gradient descent vector $-\eta\nabla L(w_{adv})$, 當作 weight $w_t$ 的 gradient step, 因此才會跑到 $w_{t+1}^{SAM}$.
先把 SAM 的 objective function 主要目的點出來, SAM 相當於希望找出來的 $w$ 其 locally 最大的 loss 都要很小, 直覺上就是希望 $w$ 附近都很平坦, 有點類似 Support Vector Machine (SVM) 的想法, 最小化最大的 loss.
以下數學推導… 數學多請服用
數學描述為:
$$\begin{align}
\min_w L_S^{SAM}(w)+\lambda\|w\|_2^2 \\
\text{where}\qquad L_S^{SAM}(w)\triangleq \max_{\|\varepsilon\|_p\leq\rho}L_S(w+\varepsilon)
\end{align}$$ 其中 $S$ 表示 training dataset, $L_S^{SAM}(w)$ 定義成 locally loss 最大的值, 其中 locally 定義為小於 $\rho$ ($p$-norm) 的球內.
多加 $\lambda||w||_2^2$ 正則項則是由 PAC (Probably Approximately Correct) Bayesian Generalization Bound (論文的 Appendix A.1) 理論推導過來的.
式 (2) 的 $L_S^{SAM}(w)$ 其近似的最佳解 $\hat\varepsilon$, 有一個有效率的 closed form 解. 利用 first-order Taylor expansion + dual norm property 推導.
$$\begin{align} \varepsilon^\ast(w)\triangleq \arg\max_{\|\varepsilon\|_p\leq\rho}L_S(w+\varepsilon) \\ \approx \arg\max_{\|\varepsilon\|_p\leq\rho} L_S(w) + \varepsilon^T\nabla_w L_S(w) \\ = \arg\max_{\|\varepsilon\|_p\leq\rho}\varepsilon^T\nabla_w L_S(w) \triangleq \hat\varepsilon(w) \end{align}$$ 式 (5) 有 closed form solution (dual norm property):
$$\begin{align} \hat{\varepsilon}(w)=\frac{\rho\cdot\text{sign}(\nabla_w L_S(w))}{\left(\|\nabla_w L_S(w)\|_q^q\right)^{1/p}}|\nabla_w L_S(w)|^{q-1} \end{align}$$ 其中 $1/q+1/p=1$, $|\cdot|^{q-1}$ 表示 element-wise 的絕對值和 power.
💡 $p$, $q$ 互為 conjugate number, 以 $p=q=2$ 來說 (6) 變成 $\hat\varepsilon(w)=\rho\cdot\nabla_w L_S(w)/|\nabla_w L_S(w)|_2$. 所以只是 $\nabla_w L_S(w)$ 的一個 positive scaling 而已, (其 negative scaling 是原來的 gradient descent direction).
所以 (1) 所需要的 gradient, $\nabla_w L_S^{SAM}(w)$ 為:
$$\begin{align} \nabla_w L_S^{SAM}(w)\approx \nabla_w L_S(w+\hat\varepsilon(w)) \\ \text{(by chain rule) } =\frac{d(w+\hat\varepsilon(w))}{dw}\left.\nabla_w L_S(w)\right|_{w+\hat\varepsilon(w)} \\ = \left(1+\frac{d \hat\varepsilon(w)}{dw}\right) \left.\nabla_w L_S(w)\right|_{w+\hat\varepsilon(w)} \\ = \left.\nabla_w L_S(w)\right|_{w+\hat\varepsilon(w)} + \frac{d \hat\varepsilon(w)}{dw}\left.\nabla_w L_S(w)\right|_{w+\hat\varepsilon(w)} \\ \approx \left.\nabla_w L_S(w)\right|_{w+\hat\varepsilon(w)} \end{align}$$ 式 (10) 到 (11) 忽略二次微分項. 論文實驗了如果把這個二次微分項也考慮進去效果反而變差?!
從 (11) 的式子來看 Figure 2 就能了解, $w_t$ 要用的 gradient 是 $w_{adv}\triangleq w+\hat\varepsilon(w)$ 這點的 gradient.
對於 SAM 來說, 一次的 weight update iteration 會跑兩次 backward, 因此論文跟原來的 SGD 對比時, 會讓 SGD iteration 數變兩倍來比較.
SAM 的 hyper-parameter 只有 $\rho$ (the neighborhood size), 論文裡用 $10\%$ of training data 當 validation set 做 search $\{0.01, 0.02, 0.05, 0.1, 0.2, 0.5\}$.
另外如果用 Data parallelism 的話, i.e. 一個大 batch 會平分成多個 sub-batch 給每個 accelarator, sub-batch 的 SAM gradients 最後在做 all-reduce (平均) 當 final SAM gradient.
實驗結果表明, 對於原來的 SGD or 有 momentum 的 optimizer (或有多加 regularization 的 loss), 如果多用了 SAM 幾乎都穩定的更好!
最後, 其實 SAM 是這篇論文推導的一個特例 “Penalizing Gradient Norm for Efficiently Improving Generalization in Deep Learning [arxiv]”. 也十分精采, 用另一種角度來看怎麼找較 flatten 的 optimal point.
References
- Sharpness-Aware Minimization for Efficiently Improving Generalization [arxiv]
- Github: (Adaptive) SAM Optimizer
- Penalizing Gradient Norm for Efficiently Improving Generalization in Deep Learning [arxiv]