剖析生成模型的 Maximum Likelihood Estimation (MLE)

Maximum likelihood estimation (MLE) 是機器學習 (ML) 中許多模型優化的目標函式
應該是大家學習 ML 一開始就接觸的內容, 但其實它可能比你想的還複雜
本文分兩大段落:
A. Maximum Likelihood Estimation (MLE):
簡單說明 MLE 後, 點出實務上會遇到的問題, 然後與 mean square error (MSE) 和 KL divergence 的關聯
B. 生成模型想學什麼:
先說明生成模型的設定, 然後帶到有隱變量的 MLE
最後點出 VAE, Diffusion (DDPM), GAN, Flow-based 和 Continuous Normalizing Flow (CNF) 這些生成模型與 MLE 的關聯

A. Maximum Likelihood Estimation (MLE)

$N$ 筆 training data $(x_i)_{i=1}^N$, MLE 要找的最佳參數 $\theta^\ast$ 為:
$$\theta^\ast=\arg\max_\theta\sum_{i=1}^N\log p_\theta(x_i)$$ 或說 MLE 在做 log-likelihood $\log p_\theta(x)$ 的最大化.

Normalization Term 計算

實務上一般寫不出公式讓我們直接計算 pdf 值 (除非用簡單的機率分佈寫得出公式的那種, 例如就高斯分佈, 這種太弱了不提)
既然如此, 那我們讓模型的輸出直接就是估計的 pdf 值不就好了?
例如有個 NN 模型 $f_\theta(\cdot)$, 輸入 $x’$ 希望輸出 $f_\theta(x’)$ 直接就是 density 值 $f_\theta(x')=p_\theta(x')$?

很難, 別忘了要成為 pdf 還要除以分母這項:
$$p_\theta(x')=\frac{f_\theta(x')}{\int_{x}f_\theta(x)dx}$$ 而 $\int_{x}f_\theta(x)dx$ 現實上根本很難算 (把所有 $x$ 都算過? $\theta$ 更新的話又得重算?)

也可參考 “Noise Contrastive Estimation (NCE) 筆記” [1] 開頭的說明

那計算不出 $p_\theta(x’)$ 該怎麼用 MLE? 滿街模型都說用 MLE 當目標函數又怎麼做到的?
最常見的一種方法是當成 regression 問題並套用 Mean Square Error (MSE)

MLE 與 Mean Square Error (MSE)

令模型的輸出為 $\hat{x}$, 而正確答案用 $x$ 表示.

$\hat{x}=f_\theta(z)$, 其中 $\theta$ 為參數.

現在有 $N$ 筆結果 $(\hat{x}_i,x_i)_{i=1}^N$. 由於模型的預測 ($\hat{x}$) 不一定準, 我們在什麼都不知道的情況下只能猜正確答案 $x$ 落在 $\hat{x}$ 附近 (用簡單的高斯分佈)

$$\begin{align} p(x|\hat{x})=\mathcal{N}(x|\hat{x},I) \end{align}$$ 所以 likelihood 為:
$$\begin{align} \text{Likelihood}=\prod_{i=1}^N p(x_i|\hat{x_i})=\prod_{i=1}^N \mathcal{N}(x_i|\hat{x_i},I) \end{align}$$ 最大化 log-likelihood 找最佳參數 $\theta$, 注意到只有 $\hat{x}$ 與 $\theta$ 有關:
$$\begin{align} \text{MLE}:=\arg\max_\theta\log\left(\prod_{i=1}^N \mathcal{N}(x_i|\hat{x_i},I)\right) \\ =\arg\max_\theta\sum_{i=1}^N \log\left(e^{-\frac{1}{2}(x_i-\hat{x}_i)^2}+\text{const.}\right) =\arg\max_\theta\left(-\frac{1}{2}\sum_{i=1}^N (x_i-\hat{x}_i)^2\right) \\ =\arg\min_\theta\sum_{i=1}^N(x_i-\hat{x}_i)^2=:\text{MSE} \end{align}$$ 得到最大化 log-likelihood (3) 等價於最小化 MSE loss (5),
因此用 MSE 可以避開不知道怎麼計算 pdf 值的問題!

MLE 與最小化 KL Divergence 等價

我們知道 KL divergence 可以量測兩個 pdf 之間的 “距離” (非數學定義的 norm)
而 MLE 學到的 $p_\theta$ 其實在做找出 $p_\theta\approx p_{data}$, 換句話說就是最小化 $KL(p_{data}\|p_\theta)$ [2]
$$\text{MLE}:=\arg\max_\theta\log\left(\prod_{i=1}^N p_\theta(x_i)\right) \\ =\arg\max_\theta\sum_{i=1}^N\log p_\theta(x_i) \approx \arg\max_\theta\mathbb{E}_{x\sim p_{data}}[\log p_\theta(x)]\\ =\arg\max_\theta \int_x p_{data}(x)\log p_\theta(x)dx -\int_x p_{data}(x)\log p_{data}(x)dx \\ = \arg\max_\theta \int_x p_{data}(x)\log\frac{p_\theta(x)}{p_{data}(x)}dx = \arg\min_\theta KL(p_{data}\|p_\theta)$$ 做 MLE 相當於在想辦法擬合資料分布

B. 生成模型想學什麼

接下來談談 VAE, Diffusion (DDPM), GAN, Flow-based 和 Continuous Normalizing Flow (CNF) 這些生成模型跟 MLE 的關聯
在開始之前還是先說清楚生成模型的設定
因為”生成”兩個字, 代表就算我們學到了模型分佈 $p_\theta$ 接近真實分佈 $p_{data}$ 的話, i.e. $p_\theta(x)\approx p_{data}(x)$, 我們還是必須想辦法從 $p_\theta$ 中採樣
即要能 sample 出 $x$ 並 follow $p_\theta$ 的分佈, 這句話數學這麼寫: $x\sim p_\theta(x)$.
然而 $p_\theta(x)$ 實際上非常複雜, 我們根本無法採樣起, 那怎麼辦呢?
生成模型的做法很聰明, 從一個我們會採樣的簡單分佈出發, 例如 $z\sim\mathcal{N}(0,I)$.
如果模型能學到如何把 $\mathcal{N}(0,I)$ 變化到目標分佈 $p_{data}(x)$, 那麼我們只需要採樣 $z$ 就可以透過模型對應到目標分佈的 $x$ 了.
(借用 Jia-Bin Huang 影片的圖 How I Understand Diffusion Models 來舉例)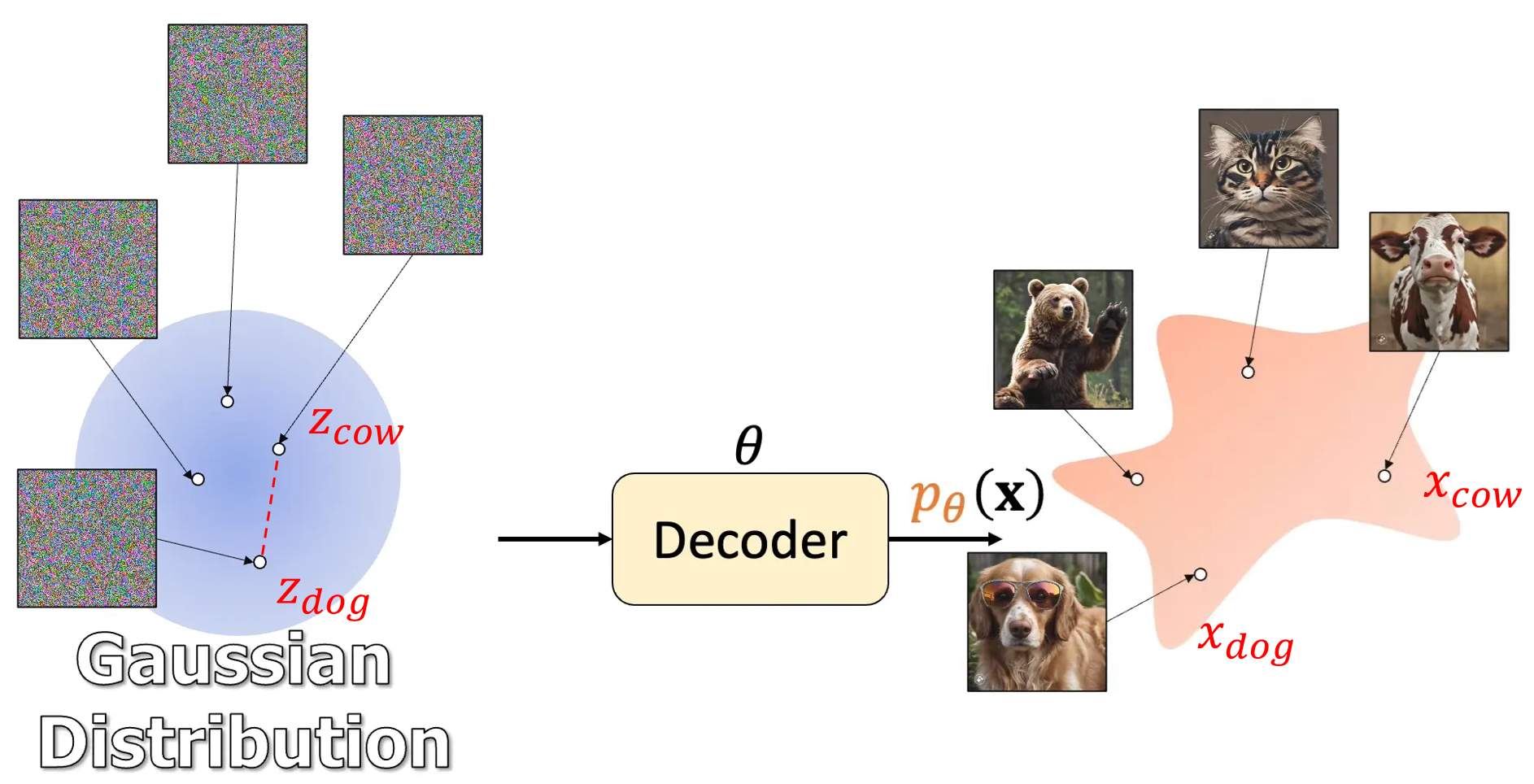
對應的關係是 $x=f_\theta(z)$ (上圖的 Decoder 就是 function $f_\theta$), 並且希望模型參數 $\theta$ 能滿足 $p_\theta(x)\approx p_{data}(x)$, 而這件事可以透過最小化 $KL(p_{data}\|p_\theta)$ 來達成. (等價 MLE)
所以因此很多生成模型目標函數都是 MLE.

有隱變量的 MLE (VAE, DDPM)

透過上面的說明我們知道生成模型引入了一個隱變量 $z\sim\mathcal{N}(0,I)$.
引入 $z$ 通常會有個特性: marginal likelihood $p_\theta(x)$ 不好算, 而 joint probability $p_\theta(x,z)=p_\theta(x|z)p(z)$ 則一般會設計得容易算.
我們用 VAE 舉例, $p(z)$ 為 Gaussian distribution 容易算, 且 $p_\theta(x|z)$ 則為 decoder 的結果. 所以 $p_\theta(x,z)$ 容易算.
或是 DDPM 中 $p_\theta(x,z)$ 為 $p(\mathbf{x}_{0:T})$ 可以直接計算 (ref [3]): $$p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \quad p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))$$ 但要算 marginal likelihood $p_\theta(x)$ 必須積分: $$p_\theta(x)=\int_zp_\theta(x,z)dz$$ 因此直接計算 $\log p_\theta(x)$ 做 MLE 變得很困難
怎麼辦呢? 我們先對 log-likelihood 改寫一下 (ref [4]): $$\log p_\theta(x)=KL(q(z)\|p_\theta(z|x))+\mathbb{E}_{z\sim q}[\log p_\theta(x,z)−\log q(z)]\\ =KL(q(z)\|p_\theta(z|x))+\mathcal{L}(q,θ)$$ 由於 $KL\geq0$, 所以 $\mathcal{L}(q,\theta)$ 這項就變成 log-likelihood 的 lower bound 了 (稱 ELBO)
透過最大化 $\mathcal{L}(q,\theta)$ 來讓我們也把 likelihood 最大化, 這也相當於達到 MLE 的目的了

不要忘記了, $\log p_\theta(x,z)$ 一般會設計得容易算, 所以 $\mathcal{L}(q,\theta)$ 也是容易計算的.

而這樣的技巧就是 VAE 和 DDPM 的做法.

GAN 的 MLE

GAN 其實非常奇耙, 不走傳統路線, 想做 MLE 但透過最小化 $KL(p_{data}\|p_\theta)$, 而想最小化 KL divergence 又透過另一個 discriminator $D$, 使得當達到 $D$ 分不出真偽時, $KL(p_{data}\|p_\theta)$ 會最小.

隔著幾層布巧妙的搔癢

Flow-based Model 的 MLE

之前提到做 MLE 因為無法直接在複雜的 $p_\theta$ 上算 pdf 值, 從而沒辦法算 likelihood.
Flow-based model 的精隨是: 如果我們的 model 能 inverse 的話, 就不用在 $p_\theta$ 上算 pdf 值, 只需要在 $\mathcal{N}(0,I)$ 上計算 pdf 值就好了!
不得不說這想法也很精彩
詳細 log-likelihood 推導請自行搜尋參考資料即可.

Continuous Normalizing Flow (CNF) 的 MLE

CNF 為 flow-based model 的連續性變化擴展. 變成使用 NN 學習 vector field $u_t(x_t,\theta)$, 而不是像 DDPM 使用 NN 學 score function [9].

用 NN 學 vector field 的方法稱為 Neural ODE [5].

從 Continuity equation (or mass conservation) (ref [6]) 出發 $$\frac{\partial p_\theta(x_t)}{\partial t}+\text{div}(p_\theta(x_t)u_t(x_t,\theta))=0$$ 可以推導出 log-likelihood, see [5] 裡的 Appendix A: Proof of the Instantaneous Change of Variables Theorem $$\frac{d\log p_\theta(x_t)}{dt}=-\text{div}(u_t(x_t,\theta))$$ 因此 log-likelihood 就是積分起來的結果: $$\log p_\theta(x)=\log p_{\text{base}}(z)+\int_{t=0}^1-\text{div}(u_t(x_t,\theta))dt$$ 所以要算 MLE 必須算上述積分項. 通常使用 numerical 積分方法 [7], e.g. Euler, Runge Kutta methods 等來積, 且因為要做 backpropagation, 這個積分的過程要能支援計算 gradient, 可想而知會非常慢! (個人很粗略地看, 有錯歡迎指正)

這也是 CNF 面臨的困難.

2023 年 Meta 一篇論文 “Flow Matching for Generative Modeling [8]” 提出了學習這個 vector field $u_t(x_t,\theta)$ 不用透過 MLE 來學, 避掉上述困難! 詳細解說看之後的 flow matching 筆記
Flow matching 是近期一項重要的生成模型技術, 比 DDPM 更 general, 訓練更快更穩定, inference 速度也更快. 許多近一兩年的模型採用此做法.如 Stable Diffusion 3, Meta 的 Voicebox, F5-TTS, CosyVoice, …

Summary

MLE 等價於 KL divergence, 而實務上可以套用使用 Gaussian noise regression 的設定變成使用 MSE 來做.
生成模型通常引入一個容易採樣的簡單分布的隱變量 $z$, 由於這個隱變量, MLE 可以藉由最大化 ELBO (likelihood 的 lower bound) 來間接最大化 likelihood.

這些生成模型 VAE, Diffusion (DDPM), GAN, Flow-based 和 Continuous Normalizing Flow (CNF) 目標雖然都是做 MLE, 但有的使用技巧卻十分隱誨且巧妙, 例如 GAN.
詳細請看內文對各個生成模型的 MLE 關聯.

而在 Bayesian learning 流派中, 如果引入參數 $\theta$ 的 prior $p(\theta)$ 分佈, 則可以更進一步探討 Maximum a posterior (MAP) 或是 Bayesian inference 等等內容. (ref [10])