接續上一篇: 讀 Flow Matching 前要先理解的東西 (建議先閱讀)
Flow matching 模型在時間 $t=0$ 的時候從常態分佈出發 $p_0(x)=\mathcal{N}(0,I)$, 隨著時間變化其 pdf, 例如時間 $t$ 時的 pdf 變化成為 $p_t(x)$, 直到時間 $t=1$ 時希望變成接近目標分佈 $q(x)$, 即希望 $p_1(x)\approx q(x)$.
概念是頭尾 pdf 確定後, 中間這無限多種可能的 $p_t(x)$ 變化經過作者的巧妙設定, 讓學 vector field $u_t(x)$ 變的可能! (不學 pdf 而是學 vector field)
結果就是用 NN 學到的 $u_t(x)$ 可以讓 pdf 從開頭的常態分佈一路變化到最後的資料目標分佈 $q(x)$.
Vector Field 決定了 Probability Path
注意到這一路變化的過程要滿足 continuity equation (質量守恆)
$$\begin{align}
\frac{\partial p_t(x)}{\partial t}
+
\nabla\cdot(p_t(x) u_t(x))=0
\end{align}$$ 其中 $u_t(x)$ 表示時間 $t$ 時在位置 $x$ 的 vector field.
而 $\nabla\cdot$ 為 Divergence (散度) 也可以這麼寫 $\text{div}$, 其定義為:
$$\text{div}(F)=\nabla\cdot F=\sum_{i=1}^n\frac{\partial F_i}{\partial x_i}$$ 其中 $F(x_1,…,x_n)=(F_1,…,F_n)$. 更多請參考: [筆記]
從 continuity equation 出發, 可推導出 Instantaneous Change of Variables Theorem [1]:
$$\frac{d\log p_t(x)}{dt}=-\nabla\cdot u_t(x)$$ 因此得到 log-likelihood, 就是積分起來的結果: $$\log p_{\color{orange}{t}}(x)=\log p_0(z)+\int_{\hat{t}=0}^{\color{orange}{t}}-\nabla\cdot u_{\hat{t}}(x) d\hat{t}$$ 因此可以發現, 如果有每個時間 $t$ 的 vector field $u_t(x)$, 透過上式就可以得到對應的 pdf $p_t(x)$.
[觀念]: Vector field $u_t(x)$ 決定了 probability path $p_t(x)$.
Flow Matching Loss
既然 $u_t(x)$ 決定了 $p_t(x)$, 讓 NN 直接學 $u_t(x)$ 就好了, 因此目標函式:
$$\mathcal{L}_{FM}(\theta)=\mathbb{E}_{t,x\sim {\color{orange}{p_t(x)}}}\|v_t(x)-{\color{orange}{u_t(x)}}\|^2, \qquad (\star)$$ 其中 $v_t(x)$ 是我們的 NN, 具有參數 $\theta$.
$t\sim U[0,1]$ 表示對任意時間 $t$ 都要去學 vector field.
注意到我們根本不知道真實的 ${\color{orange}{u_t(x)}}$ 和 ${\color{orange}{p_t(x)}}$, 所以 $\mathcal{L}_{FM}$ 該怎麼計算?
High level picture 的想法是, 我們定義出頭尾分佈, 頭的分佈就用標準常態分佈, 尾的分佈從 training data 設計出來. 中間變化的分佈論文經過特殊設計.
設計好後, 就能找出 ${\color{orange}{u_t(x)}}$ 和 ${\color{orange}{p_t(x)}}$ 了, 找出來後應該就有機會算 $\mathcal{L}_{FM}$ 了.
以下詳細說明.
頭尾的分佈長相
我們先來想像一下怎麼從 $\mathcal{N}(0,I)$ 一路轉換成目標分佈 $q(x)$.
假設我們有 $N$ 筆 training data $x_1=\{x_1^1,x_1^2,...,x_1^N\}$.
對第 $n$ 筆資料 $x_1^n$, 設定 $t=0$ 時條件機率分佈:
$$\begin{align}
p_0(x|x_1^n)=p_0(x)=\mathcal{N}(0,I)
\end{align}$$ 也就是初始分佈與資料無關, 全部都是標準常態分佈
接著設定 $t=1$ 時條件機率分佈:
$$\begin{align}
p_1(x|x_1^n)=\mathcal{N}\left(x_1^n,\sigma_{min}^2I\right)
\end{align}$$ 並假設每一筆訓練資料機率相同, $q(x_1^n)=1/N,\forall n=1,2,...,N$. 則
$$p_1(x)=\sum_{n=1}^N p_1(x|x_1^n)q(x_1^n)\\
=\frac{1}{N}\sum_{n=1}^N p_1(x|x_1^n)=\frac{1}{N}\sum_{n=1}^N \mathcal{N}\left(x_1^n,\sigma_{min}^2I\right)$$ 這是個 Gaussin Mixture Model (GMM) 分佈
理論上 $N\rightarrow\infty,\sigma_{min}\rightarrow0$ 時 $p_1(x)$ 就會等於目標分佈 $q(x)$. 或我們寫成連續積分形式
$$\begin{align}
p_1(x)=\int p_1(x|x_1)q(x_1)dx_1
\end{align}$$ 其中 $p_1(x|x_1)=\mathcal{N}(x_1,\sigma_{min}^2I)$, $q(x_1)$ 是目標分佈, 也就是從手上的 training data 採樣就可以.
事實上 $q(x_1)$ 可以設定的很彈性, 不一定要從 training data 採樣. 更廣泛來說下式數學上本就成立:
$$p_1(x)=\int p_1(x|{\color{orange}{z}})q({\color{orange}{z}})d{\color{orange}{z}}$$ $z$ 可以是很彈性的變量, 而 $q(z)$ 是它的 distribution.
現在我們先想成 $z$ 就是 training data $x_1$ 即可. $q(z)$ 就是目標分佈 $q(x_1)$, 即手上的 data 分佈
後面會說明 $z$ 和 $q(z)$ 的其他選擇.
任何時間 $t$ 都可以這樣寫: $$\begin{align}
p_{\color{orange}{t}}(x)=\int p_{\color{orange}{t}}(x|x_1)q(x_1)dx_1
\end{align}$$ 因此我們設定好了式 (2) 的頭 $p_0(x)$ 和式 (4) 的尾 $p_1(x)$ 的分佈
中間分佈的設定
由式 (2) 和 (4) 我們設定好了頭尾分佈, 那中間的 pdf $p_t(x)$ 怎麼設定?
或是因為 $u_t(x)$ 決定了 $p_t(x)$, 我們改問 $u_t(x)$ 怎麼設定?
可以想像有無窮多種 $u_t(x)$ 的設定方法 (因為只要滿足頭尾 pdf 即可)
但還是要有個變化規則, 這樣 NN 才知道要學什麼.
$u_t(x)$ 的規則是 (注意到這是人為定義的):
$$\begin{align}
u_t(x) \triangleq \int u_t(x|x_1)\frac{p_t(x|x_1)q(x_1)}{p_t(x)}dx_1
\end{align}$$ 怕大家看到這裡忘記: $x_1$ 是訓練資料 $\{x_1^1,x_1^2,...,x_1^N\}$, 然後 $q(x_1)$ 表示目標分佈 (資料分佈).
其中特別說明 $u_t(x|x_1)$ 與 $p_t(x|x_1)$ 是一對的, 也就是說 $u_t(x|x_1)$ 產生 $p_t(x|x_1)$ 因此需滿足質量守恆 continuity equation (1). 這裡我們先假設已經有這樣一對的東西.
因為 $u_t(x)$ 是人為定義, 我們需要驗證它是合法的 vector field, i.e. 能產生 $p_t(x)$ (5), 即要滿足 continuity equation (1). 證明放在 Appendix.
因此得到 $u_t(x)$ 和 $p_t(x)$ 是一對的, 式 (6) 定義的 $u_t(x)$ 是 well-defined.
不過我們仍不知道 (6) 中的 $u_t(x|x_1)$ 和 $p_t(x|x_1)$ 的長相, 論文直接定義 $p_t(x|x_1)$ 長這樣:
$$\begin{align}
p_t(x|x_1)\triangleq\mathcal{N}\left(
\mu_t(x_1),\sigma_t(x_1)^2I
\right)
\end{align}$$ Mean 和 covariance matrix 都是 $x_1$ 的函數.
這樣定義後有個問題, 什麼長相的 $u_t(x|x_1)$ 會產生式 (7) $p_t(x|x_1)$ 的定義?
論文的 Theorem 3 證明了存在唯一 $u_t(x|x_1)$ 產生式 (7) $p_t(x|x_1)$:
$$\begin{align}
u_t(x|x_1)=\frac{\dot{\sigma_t}(x_1)}{\sigma_t(x_1)}(x-\mu_t(x_1))+\dot{\mu_t}(x_1)
\end{align}$$ 其中 $\dot\sigma_t$ 和 $\dot\mu_t$ 分別表示 $\sigma_t$ 和 $\mu_t$ 對 $t$ 偏微分. 證明放在 Appendix
這結果實在太方便了, 基本上只要把 $\mu_t$ 和 $\sigma_t$ 定義好, $u_t(x|x_1)$ 有 closed form solution!
講到現在可能有點亂了, 整理一下目前的故事線:
定義了條件機率 $p_t(x|x_1)$ 的長相後 (7), 我們可以得到存在唯一的條件向量場 $u_t(x|x_1)$ 長相 (8)
有了 $p_t(x|x_1)$ 和 $u_t(x|x_1)$, 我們就能得出向量場 ${\color{orange}{u_t(x)}}$ (6) 和 ${\color{orange}{p_t(x)}}$ (5).
Flow matching loss $\mathcal{L}_{FM}(\theta)$ 就能計算了!
$$\begin{align}
\mathcal{L}_{FM}(\theta)=\mathbb{E}_{t,x\sim {\color{orange}{p_t(x)}}}\|v_t(x)-{\color{orange}{u_t(x)}}\|^2
\end{align}$$ 真的能算… 吧? 是吧?
好像還是不行, (5) 和 (6) 這樣的積分形式很難算.
Conditional Flow Matching Loss
論文的再一個重要發現為把 $\mathcal{L}_{FM}$ 轉為等價且實際可計算的 loss, a.k.a. Cnditional Flow Matching $\mathcal{L}_{CFM}$:
$$\begin{align}
\mathcal{L}_{CFM}(\theta)=\mathbb{E}_{t,q(x_1),{\color{orange}{p_t(x|x_1)}}}\|v_t(x)-{\color{orange}{u_t(x|x_1)}}\|^2
\end{align}$$ 由於 ${\color{orange}{p_t(x|x_1)}}$ 和 ${\color{orange}{u_t(x|x_1)}}$ 很容易計算 (式 (7), (8)), 因此 $\mathcal{L}_{CFM}$ 很容易算
論文證明 $\nabla_\theta\mathcal{L}_{CFM}(\theta)=\nabla_\theta\mathcal{L}_{FM}(\theta)$! 證明放在 Appendix.
Gradient 一樣, 因此找出來的最佳解 $\theta$ 也一樣.
有意思的是 $\mathcal{L}_{CFM}$ 用的 ground truth 是 conditional vector field $u_t(x|x_1)$, 但是這樣學出來的 $v_t(x)$ 卻是等價於去逼近原本的 (unconditional) vector field $u_t(x)$! 重點是 $\mathcal{L}_{CFM}$ 又容易計算.
Conditional Probability 和 Conditional Vector Field 的選擇
條件分佈 $p_t(x|x_1)$ 如下設定後會有唯一的條件向量場 $u_t(x|x_1)$:
$$p_t(x|x_1)\triangleq\mathcal{N}\left(
\mu_t(x_1),\sigma_t(x_1)^2I
\right) \\
u_t(x|x_1)=\frac{\dot{\sigma_t}(x_1)}{\sigma_t(x_1)}(x-\mu_t(x_1))+\dot{\mu_t}(x_1)$$ $\dot\sigma_t$ 表示 $\sigma_t$ 對 $t$ 偏微分, $\dot\mu_t$ 表示 $\mu$ 對 $t$ 偏微分. (證明放在 Appendix)
這樣的設定能讓我們方便計算 $\mathcal{L}_{CFM}$ (等價於 $\mathcal{L}_{FM}$).
同時保證 NN 學出來的 $v_t(x)$ 其對應的 $p_t(x)$ 能滿足頭是標準常態分佈, 尾是目標分佈. (其實頭分佈不一定要是標準常態, 以下段落會說明)
因此我們可以設計不同的 $\mu_t$ 和 $\sigma_t$, 就可以有不同的中間 pdf $p_t$ 演變方式.
Conditional flows from FM (Lipman et al.)
選擇 conditional probability path $p_t(x|x_1)$ 的 $\mu_t,\sigma_t$ 為:
$$\mu_t(x)=tx_1 \\
\sigma_t(x)=1-(1-\sigma_{min})t$$ 套 (8) 得到具有唯一的 conditional vector field $u_t(x|x_1)$:
$$u_t(x|x_1)=\frac{x_1-(1-\sigma_{min})x}{1-(1-\sigma_{min})t}$$ 讀者可自行對 $\mu_t$ 和 $\sigma_t$ 對 $t$ 偏微分驗證.
對於這裡的 $\mu_t,\sigma_t$ 我們設定 $t=0$ 和 $t=1$ 觀察得到
$$\mu_0(x_1)=0,\quad \sigma_0(x_1)=1 \\
\mu_1(x_1)=x_1,\quad \sigma_1(x_1)=\sigma_{min}$$ 代入到 (7) 得到
$$p_0(x|x_1)=\mathcal{N}(0,I) \\
p_1(x|x_1)=\mathcal{N}(x_1,\sigma_{min}^2I)$$ 我們觀察最終 marginal 後的頭尾分佈 $p_0(x),p_1(x)$
$$p_0(x)=\int_{x_1}p_0(x|x_1)q(x_1)dx_1=\mathcal{N}(0,I)\int_{x_1}q(x_1)dx_1=\mathcal{N}(0,I) \\
p_1(x)=\int_{x_1}p_1(x|x_1)q(x_1)dx_1=\int_{x_1}\mathcal{N}(x_1,\sigma_{min}^2I)q(x_1)dx_1$$ 正好就是頭分佈為 standard Gaussian (2) 而尾分佈是 training data 形成的 Gaussian mixture model (GMM) 式 (4)
見論文 [2] 的圖如下: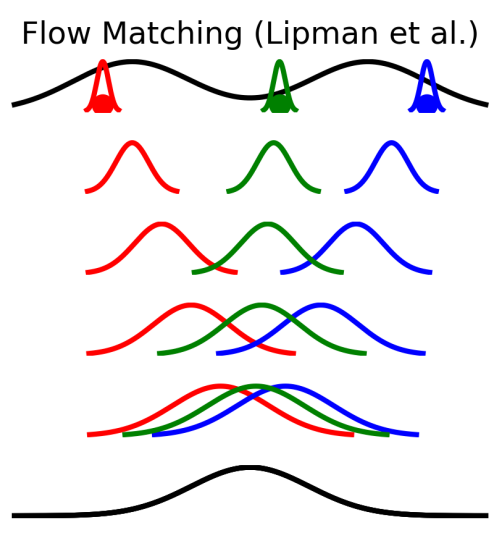 可以看到開頭大家都是 standard Gaussian 然後漸漸演變到各自的位置
可以看到開頭大家都是 standard Gaussian 然後漸漸演變到各自的位置
I-CFM (Independent Coupling)
注意到前面推導的 $x_1$ 都可以用更廣泛的 random variable $z$ 來套用, 數學都成立!
所以我們令 ${\color{orange}{z\triangleq(x_0,x_1)}}$ 且 $x_0$ 從一個使用者自定義的一個容易採樣的分佈 $p_0(x_0)$ 去採樣, $x_1$ 從目標分佈 $q$ (training data 的分佈) 去採樣
並且讓 $x_0$ 和 $x_1$ 獨立採樣:
$$q({\color{orange}{z}})\triangleq p_0(x_0)p_1(x_1)$$ 則選擇 conditional probability path $p_t(x|z)$ 的 $\mu_t,\sigma_t$ 為:
$$\mu_t({\color{orange}{z}})=tx_1+(1-t)x_0 \\
\sigma_t({\color{orange}{z}})=\sigma_{min}$$ 套 (8) 得到具有唯一的 conditional vector field $u_t(x|{\color{orange}{z}})$:
$$u_t(x|{\color{orange}{z}})=x_1-x_0$$ 詳細可參考論文 [2]
此時一樣觀察 $t=0$ 和 $t=1$ 的 $\mu_t,\sigma_t$:
$$\mu_0({\color{orange}{z}})=x_0,\quad \sigma_0({\color{orange}{z}})=\sigma_{min} \\
\mu_1({\color{orange}{z}})=x_1,\quad \sigma_1({\color{orange}{z}})=\sigma_{min}$$ 同樣地代入到 (7) 得到
$$p_0(x|{\color{orange}{z}})=\mathcal{N}(x_0,\sigma_{min}^2I) \\
p_1(x|{\color{orange}{z}})=\mathcal{N}(x_1,\sigma_{min}^2I)$$ 我們觀察最終 marginal 後的頭分佈 $p_0(x)$:
$$p_0(x)=\int_{\color{orange}{z}}p_0(x|{\color{orange}{z}})q({\color{orange}{z}})d{\color{orange}{z}}=\int_{x_0}\int_{x_1}\mathcal{N}(x_0,\sigma_{min}^2I)p_0(x_0)p_1(x_1)d{x_1}d{x_0} \\
=\left(\int_{x_0}\mathcal{N}(x_0,\sigma_{min}^2I)p_0(x_0)dx_0\right) \left(\int_{x_1}p_1(x_1)d{x_1}\right)=\int_{x_0}\mathcal{N}(x_0,\sigma_{min}^2I)p_0(x_0)dx_0$$ 注意到 $p_0(x_0)$ 是使用者預先定義好的一個容易採樣的分佈
則可以將 $p_0(x)$ 想成是一個 GMM 分佈, 每一個從 $p_0(x_0)$ 採樣出來的點 $x_0$ 都是 $\mathcal{N}(x_0,\sigma_{min}^2I)$ 的”小Gaussian”.
因此廣義上來說, 真正得頭分佈 $p_0(x)$ (注意不是 $p_0(x_0)$ 喔) 不一定都要從 standard Gaussian 出發, 只要 $p_0(x_0)$ 是我們容易採樣的任意分佈就可以, 這樣衍生出來的 $p_0(x)$ 只是根據 $p_0(x_0)$ 多疊加了”小Gaussian”而已, 有點像把分佈再”模糊一下”.
尾分佈的推導也是一個 GMM 分佈, 每一個從 $p_1(x_1)$ (資料分布) 採樣出來的點 $x_0$ 都為 $\mathcal{N}(x_0,\sigma_{min}^2I)$ 的”小Gaussian”.
當 $p_0(x_0)$ 定義為 standard Gaussian 時, 有論文 [2] 的圖如下: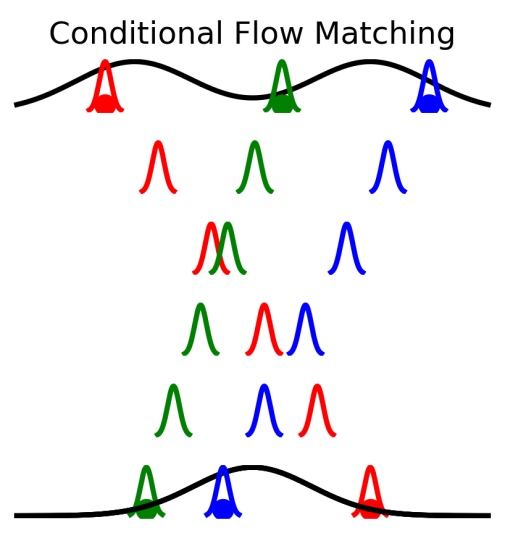 可以看到有那些 “小Gaussian”, 這與 Lipman 的設定不同.
可以看到有那些 “小Gaussian”, 這與 Lipman 的設定不同.
OT-CFM (Optimal transport)
選擇 conditional probability path $p_t(x|{\color{orange}{z}})$ 的 $\mu_t,\sigma_t$ 為:
$$\mu_t({\color{orange}{z}})=tx_1+(1-t)x_0 \\
\sigma_t({\color{orange}{z}})=\sigma_{min}$$ 其中 ${\color{orange}{z\triangleq(x_0,x_1)}}$ 這與 I-CFM 一樣, 不同的是此時的 $x_0$ 和 $x_1$ 不再是獨立採樣, 而是根據 2-Wasserstein distance, 即最小搬運 cost, 詳細參考論文 [2], 圖如下: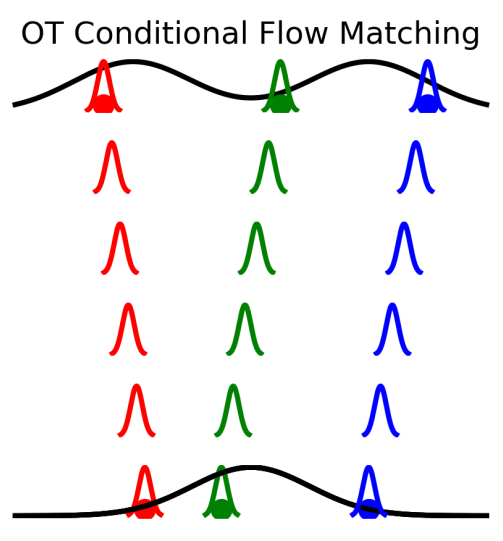 譬如圖中一次選擇了 3 個 $x_0$, 和 3 個 $x_1$, 由 OT 來決定怎麼找出最佳配對.
譬如圖中一次選擇了 3 個 $x_0$, 和 3 個 $x_1$, 由 OT 來決定怎麼找出最佳配對.
同時論文也展示了頭分佈為一個 8 個 mixtures 的 GMM, 而尾分佈為螺旋分佈: 明顯看到經過 OT 的分配路徑的演變簡單得多, 論文也說明這會更穩定也更容易訓練.
明顯看到經過 OT 的分配路徑的演變簡單得多, 論文也說明這會更穩定也更容易訓練.
Inference and Sampling
我們花了大把的篇幅來說明怎麼學 vector field $u_t(x)$.
如同 “讀 Flow Matching 前要先理解的東西” 說的 vector field 我們想成是速度的話, 理論上時間 $t$ 時 $p_t(x)$ 的任一點 $x_t$ 都能夠得出演變的路徑.
$$\frac{d}{dt}x_t=u_t(x_t)$$ 這個路徑我們叫 flow.
因此採樣就是從 $p_0(x)$ 出發得到一個點 $x_0$, 離散的估計 $\Delta t$ 時間後的位置為:
$$x_{\Delta t}=x_0+\frac{d}{dt}x_0\cdot \Delta t \\
=x_0+u_0(x_0)\cdot \Delta t$$ 所以時間 $t$ 時, $t+\Delta t$ 的位置為:
$$x_{t+\Delta t}=x_t+\frac{d}{dt}x_t\cdot \Delta t \\
=x_t+u_t(x_t)\cdot \Delta t$$ 當 $\Delta t$ 每次都走很小步的時候就會比較準, 但要花很多次 iteration.
這種 Naive 的方法為 Euler method.
實際上有更多好的選擇, 請參考 [4] Numerical Methods for Ordinary Differential Equations
Toy Example Codes
這篇文章 “Flow Matching: Matching flows instead of scores” [3] 有給出 Conditional flows from FM (Lipman) 和 I-CFM 的 sample codes. 完整 source code 在 [6].
算是一個很清楚的展示, 容易擴展.
Flow matching 理論雖然複雜精美, 實作上卻十分簡潔! 精彩!
Appendix
證明直接擷取自論文 [5], 為了完整性做紀錄而已
Vector field 決定了 probability path
證明 $u_t(x)$ 能產生 $p_t(x)$
證明存在唯一 $u_t(x|x_1)$ 產生式 (7) $p_t(x|x_1)$
先說明一個觀念, vector field $u_t(x)$ 我們可以想成速度, 即位置對時間的微分, 有了速度就可以知道下一個時間點的位置
因此隨著時間變化的位置稱為 flow $\phi_t(x)$, 則 $d\phi_t(x)/dt=u_t(\phi_t(x))$.
同樣的對 conditional vector field $u_t(x|z)$ 想成速度的話, 下一個時間點的位置為 conditional flow $\psi_t(x|z)$, 滿足:
$$\begin{align}
d\psi_t(x|z)/dt=u_t(\psi_t(x|z)|z)
\end{align}$$ 以下為定理描述
[Thm]:
定義 $\mu_0(z)=0$, $\mu_1(z)=z$, $\sigma_0(z)=1$, and $\sigma_1(z)=\sigma_{min}$ (此條件表示頭分佈為 Standard Normal, 尾分佈為接近資料分布的 GMM, 見上面 “頭尾的分佈長相“ 的段落).
試證明當條件向量場 $u_t(x|z)$ 為下式時 ($\dot{\mu_t}$ 表示 $\mu_t$ 對 $t$ 篇微分, 同理 $\dot{\sigma_t}$):
$$\begin{align}
u_t(x|z)=\frac{\dot{\sigma_t}(z)}{\sigma_t(z)}(x-\mu_t(z))+\dot{\mu_t}(z)
\end{align}$$ 此條件向量場所得到的條件機率 $p_t(x|z)$ 滿足此 Gaussian probability path:
$$\begin{align}
p_t(x|z)\sim\mathcal{N}(\mu_t(z),\sigma_t^2(z)I)
\end{align}$$ [Proof]: (注意到這裡我們捨棄論文裡的證明方式, 看不太懂, 改從 “An Introduction to Flow Matching and Diffusion Models“ p17 Example 11 筆記下來)
給定 $z$ 條件下, 讓我們設定 $x$ 在時間 $t$ 時的位置函數為:
$$\begin{align}
\psi_t(x|z)=\mu_t(z)+\sigma_t(z)x
\end{align}$$ 則因為頭分佈是 Standard Normal distribution, $X_0\sim\mathcal{N}(0,I)$, 則
$$\begin{align*}
X_t=\psi_t(X_0|z)=\mu_t(z)+\sigma_t(z)X_0\sim\mathcal{N}(\mu_t(z),\sigma_t^2(z)I)=p_t(X|z)
\end{align*}$$ 所以如果位置更新的方法使用式 (14), 那麼就滿足我們要的 conditional probability path $p_t(\cdot|z)$ 要求 (式 (13))
再來只需找出 (14) 對應的 (conditional) vector field $u_t(x|z)$ 即可.
$$\begin{align*}
\frac{d}{dt}\psi_t(x|z)=u_t(\psi_t(x|z)|z),\quad \forall x, z,\quad \text{by (11)} \\
\Longrightarrow \dot{\mu_t}(z)+\dot{\sigma_t}(z)x=u_t(\mu_t(z)+\sigma_t(z)x|z),\quad \text{by (14)} \\
\end{align*}$$ Let $x'\triangleq\mu_t(z)+\sigma_t(z)x \Leftrightarrow x=(x'-\mu_t(z))/\sigma_t(z)$ 代回去得到
$$\begin{align*}
\Longrightarrow \dot{\mu_t}(z)+\dot{\sigma_t}(z)
\left(\frac{x'-\mu_t(z)}{\sigma_t(z)}\right)=u_t(x'|z) \\
\Longrightarrow u_t(x|z)=\frac{\dot{\sigma_t}(z)}{\sigma_t(z)}(x-\mu_t(z))+\dot{\mu_t}(z)
\end{align*}$$ Q.E.D.
最後一個推導只是重新把 $x’$ 改命名為 $x$ 然後整理一下而已.
最後, 如果使用者設定 $\mu_t(z)=\mu_tz$ ($z$ 的線性函數), 條件向量場 $u_t(x|z)$ (12) 可改寫為以下形式:
$$\begin{align*}
\frac{\dot{\sigma_t}(z)}{\sigma_t(z)}x +
\left(
\dot{\mu_t} - \frac{\dot{\sigma_t}(z)}{\sigma_t(z)}\mu_t
\right)z
\end{align*}$$ 相當於看作是 $x$ 和 $z$ 的線性組合
Conditional FM 與 FM Losses 等價
考慮 FM (9) and CFM (10) 的 loss norm 為 L2 or L1 norm 兩種情形:
- CFM Loss (10) 的 norm 如果為 L2-norm 的話, 試證明 $\nabla_\theta\mathcal{L}_{CFM}(\theta)=\nabla_\theta\mathcal{L}_{FM}(\theta)$ 或等價於證明 $\mathcal{L}_{FM}(\theta)=\mathcal{L}_{CFM}(\theta) + C$, 其中 $C$ 為與 $\theta$ 無關的 constant.
- 而如果 Loss (9) and (10) 採用 L1-norm 的話, 試證明 $\mathcal{L}_{FM}(\theta)\leq\mathcal{L}_{CFM}(\theta)$, 因此 minimize $\mathcal{L}_{CFM}(\theta)$ 也能等效於降低 $\mathcal{L}_{FM}(\theta)$.
在 bilibili 開發的 IndexTTS2 (arxiv, 官網, Github) 裡面的 CFM loss 選用的是 L1-norm
以下L2-norm 的證明從 An Introduction to Flow Matching and Diffusion Models (Theorem 18) 節錄
L1-norm 的結論和證明為筆者自己推導, 在這門課程的 [colab 作業2] 中實作後能學到正確的 distribution, 讀者可以嘗試看看.
一些 notation 改動:
- 為了簡潔, 我們寫 $\mathbb{E}_{t\sim\text{Unif}}$ 為 $\mathbb{E}_{t}$, 其中 $t\sim\text{Unif}$ 表示 $t$ 從 $[0,1]$ 的均勻分布採樣而來.
- 將 L2-norm $\|\cdot\|_2$ 簡寫成 $\|\cdot\|$, 而 L1-norm 維持
- 同時為了強調出 NN 的參數 $\theta$, 將 $v_t(x)$ 改寫為 $v_t^\theta(x)$.
- $u_t(x)$ 仍然為目標的(要學的) vector field.
[Proof 當 Loss 為 “L2-norm”]:
證明過程只需將 mean square error 展開並移除與參數無關的項
$$\begin{align*}
\mathcal{L}_{FM}(\theta)=\mathbb{E}_{t,x\sim p_t}[\|v_t^\theta(x)-u_t(x)\|^2] \\
= \mathbb{E}_{t,x\sim p_t}[\|v_t^\theta(x)\|^2 - 2v_t^\theta(x)^Tu_t(x) + \|u_t(x)\|^2] \\
= \mathbb{E}_{t,x\sim p_t}[\|v_t^\theta(x)\|^2] - 2\mathbb{E}_{t,x\sim p_t}[v_t^\theta(x)^Tu_t(x)] + C_1 \\
= \mathbb{E}_{t,z\sim q,x\sim p_t(\cdot|z)}[\|v_t^\theta(x)\|^2] - 2 {\color{orange}{\mathbb{E}_{t,x\sim p_t}[v_t^\theta(x)^Tu_t(x)]}} + C_1
\end{align*}$$ 其中 $C_1$ 是一個與 $\theta$ 無關的 constant. 我們將中間橘色的 term 拆開來推導:
$$\begin{align*}
\mathbb{E}_{t,x\sim p_t}[v_t^\theta(x)^Tu_t(x)] = \int_0^1\int p_t(x) v_t^\theta(x)^Tu_t(x) \,dx\,dt \\
\text{by (6)}\quad = \int_0^1\int p_t(x) v_t^\theta(x)^T \left[ \int u_t(x|z)\frac{p_t(x|z)q(z)}{p_t(x)} \,dz \right] \,dx\,dt \\
= \int_0^1\int\,\int v_t^\theta(x)^Tu_t(x|z)p_t(x|z)q(z)\,dz\,dx\,dt \\
=\mathbb{E}_{t,z\sim q,x\sim p_t(\cdot|z)}[v_t^\theta(x)^Tu_t(x|z)]
\end{align*}$$ 代回去變成:
$$\begin{align*}
\mathcal{L}_{FM}(\theta) = \mathbb{E}_{t,z\sim q,x\sim p_t(\cdot|z)}[\|v_t^\theta(x)\|^2] - 2\mathbb{E}_{t,z\sim q,x\sim p_t(\cdot|z)}[v_t^\theta(x)^Tu_t(x|z)] + C_1 \\
= \mathbb{E}_{t,z\sim q,x\sim p_t(\cdot|z)}[\|v_t^\theta(x)\|^2-2v_t^\theta(x)^Tu_t(x|z)+\|u_t(x|z)\|^2 - \|u_t(x|z)\|^2] + C_1 \\
= \mathbb{E}_{t,z\sim q,x\sim p_t(\cdot|z)}[\|v_t^\theta(x)\|^2-2v_t^\theta(x)^Tu_t(x|z)+\|u_t(x|z)\|^2] + C_2 + C_1 \\
= \mathbb{E}_{t,z\sim q,x\sim p_t(\cdot|z)}[\|v_t^\theta(x)-u_t(x|z)\|^2]+C_2+C_1 \\
= \mathcal{L}_{CFM}(\theta) + C \\
\square
\end{align*}$$ Q.E.D.
[Proof 當 Loss 為 “L1-norm”]:
注意到 (conditional) vector field $v_t^\theta(x)$ 和 $u_t(x)$ 是一個 $d$-dim 的向量. 多一個下標 $i$ 表示第 $i$ 維.
$$\begin{align*}
\mathcal{L}_{FM}(\theta)=\mathbb{E}_{t,x\sim p_t}[\|v_t^\theta(x)-u_t(x)\|_1] \\
= \mathbb{E}_{t,x\sim p_t}\left[ \sum_i |v_{t,i}^\theta(x)-u_{t,i}(x)| \right] \\
=\int_0^1\int p_t(x)\left(\sum_i |v_{t,i}^\theta(x)-u_{t,i}(x)|\right)dx\,dt \\
=\int_0^1\int p_t(x)\left(\sum_i \left|v_{t,i}^\theta(x)-\int u_{t,i}(x|z)\frac{p_t(x|z)q(z)}{p_t(x)}dz\right|\right)dx\,dt \\
=\int_0^1\int \sum_i\left|p_t(x)v_{t,i}^\theta(x) - \int u_{t,i}(x|z)p_t(x|z)q(z)\,dz\right|\,dx\,dt \\
=\int_0^1\int \sum_i\left|\int v_{t,i}^\theta(x)p_t(x|z)q(z)\,dz - \int u_{t,i}(x|z)p_t(x|z)q(z)\,dz\right|\,dx\,dt
\end{align*}$$ 上面最後一行是由於 $p_t(x)=\int p_t(x|z)q(z)\,dz$ 而來, 繼續推導:
$$\begin{align*}
=\int_0^1\int \sum_i\left|\int (v_{t,i}^\theta(x)-u_{t,i}(x|z))p_t(x|z)q(z)\,dz \right|\,dx\,dt \\
\leq\int_0^1\int\sum_i \left(\int|v_{t,i}^\theta(x)-u_{t,i}(x|z)|p_t(x|z)q(z)\,dz\right) \,dx\,dt \\
=\int_0^1\int\,\int \left(\sum_i|v_{t,i}^\theta(x)-u_{t,i}(x|z)|\right) p_t(x|z)q(z)\,dz\,dx\,dt \\
=\int_0^1\int\,\int \|v_t^\theta(x)-u_t(x|z)\|_1 \,dz\,dx\,dt \\
= \mathbb{E}_{t,z\sim q,x\sim p_t(\cdot|z)}\|v_t^\theta(x)-u_t(x|z)\|_1=\mathcal{L}_{CFM}(\theta) \\
\Longrightarrow \mathcal{L}_{FM}(\theta)\leq\mathcal{L}_{CFM}(\theta) \\
\square
\end{align*}$$ Q.E.D.
Reference
- Neural Ordinary Differential Equations, Appendix A: Proof of the Instantaneous Change of Variables Theorem
- Improving and generalizing flow-based generative models with minibatch optimal transport [arxiv]
- Flow Matching: Matching flows instead of scores
- Numerical Methods for Ordinary Differential Equations
- Flow Matching for Generative Modeling [arxiv]
- Toy Example Codes from [here]
- 20250822 更新: Introduction to Flow Matching and Diffusion Models 這門 MIT 的課程超級棒!! 將之前許多散亂的知識點系統性串再一起, 譬如 flow matching 和 score matching 的關聯, Fokker-Planck Equation 和 Continuity Equation 的關聯, Langevin dynamics 的關聯等等!