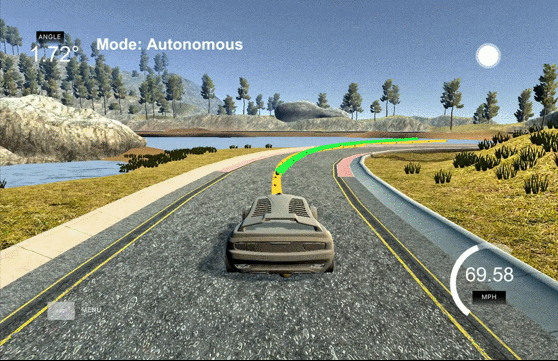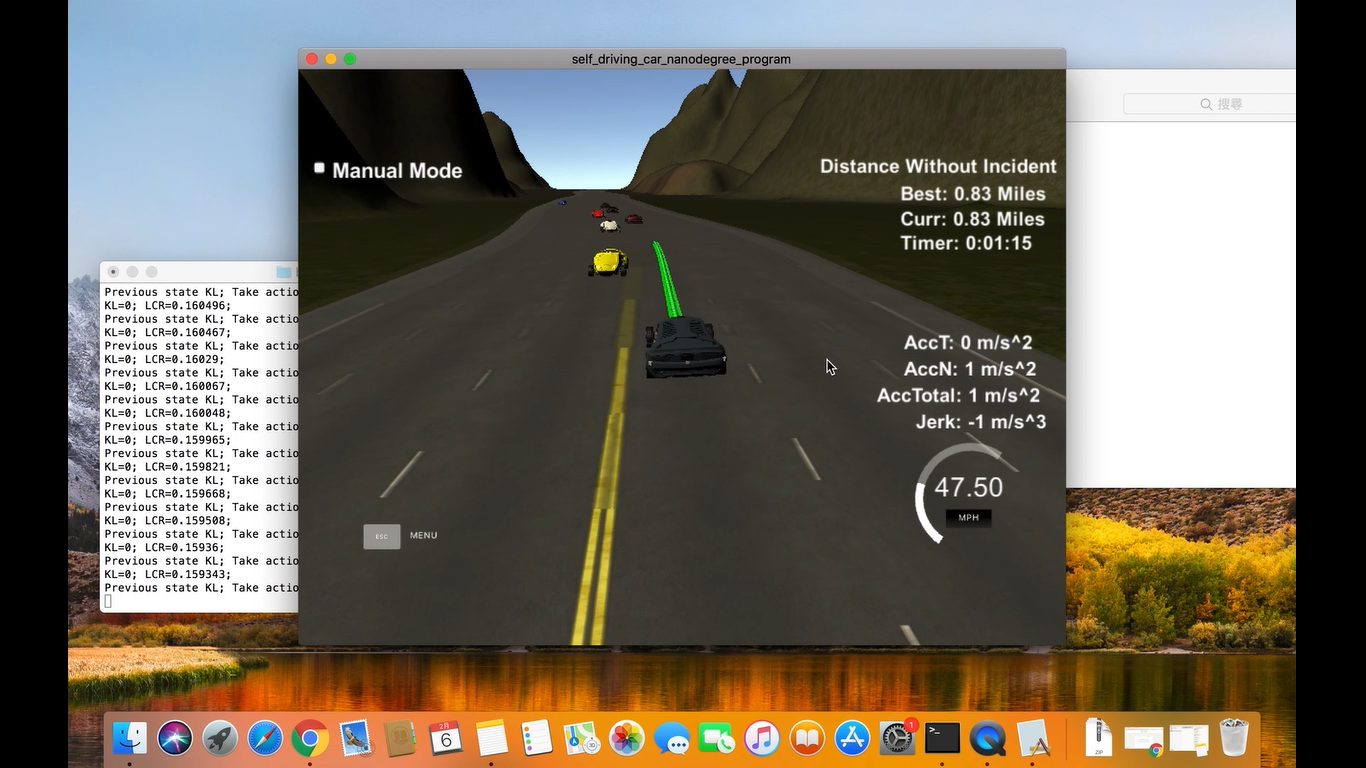
停了半年 的 Udacity Self Driving Car (SDC) Program, 終於又開始了. 做為 Term3 的第一個 Project, 我抱著高度的期待. 不過完成後, 有點小失望. 失望的原因是這個 project 跟課程上的連結感覺不是那麼明顯. 例如課程上有講到 A*, hybrid A* 的算法, 但 project 是模擬 highway drive, 因此 A* 比較不適合 (適合在 parking lot 場景). 另外也有提到怎麼降低 jerk (加速度的微分, 主要是不舒適的來源), 當參考內容是很好, 不過在寫 Project 時感覺也不大需要.
這篇就是個紀錄, 會很水. 方法很簡單, 一張圖解決:
Maximum Mutual Information (MMI) 序列的鑑別性訓練方法從早期的 GMM-HMM, 到現今就算使用了深度學習同樣十分有用, 如 Kaldi chain model 在 DNN-HMM 的基礎上加上序列鑑別訓練, 性能會再進一步提升. 前一陣子讀了俞棟、鄧力的這本 語音識別實踐, 對我來說整理得滿好的, 就是數學部分的推導有點簡潔了些, 所以這篇就基於該書的推導, 補齊了較詳細的步驟, 並且嘗試使用 Computational graph 的方式理解 MMI 的訓練. 那麼就開始吧!
用自己畫的 MMI 的計算圖譜當封面吧 :)
這篇介紹 computational graph (計算圖譜), 主要來源參考自李宏毅教授的課程內容. 並且我們使用 tensorflow 的求導函數 tf.gradients 來驗證 computational graph. 最後我們在 MNIST 上驗證整個 DNN/CNN 的 backpropagation 可以利用 computational graph 的計算方式訓練.
2011年自己做的筆記, 放上來以免檔案丟失, 也方便隨時參考. 參考自 “Numerical Optimization” by Jorge Nocedal and Stephen J. Wright. 但是打算只用 Lagrange Multiplier Theorem 理解 KKT. :)
就像是一般微積分裡學到的一樣, 對於一個函式 $f(x)$ 若 $x^\ast$ 為一 minimal/maximum point, 則必要條件為 $f’(x^\ast)=0$. 而在 constraint optimization 版本必要條件變成 KKT conditions. 說更清楚一點就是, 若 $x^\ast$ 為一 minimal/maximum point (+滿足某些神秘條件) , 則必要條件為在 $x^\ast$ 滿足 KKT Conditions.
神秘條件稱為 Constraint Qualifications, 常見的為 LICQ, 在 Convex opt 裡為 Slater’s condition. wiki KKT
具體來說，我們要探討的是對於以下的問題，如果 $x^\ast$ 為一 minimal point 且滿足式 (2) 的條件, 則會發生什麼事情 (我們找的是必要條件)
$$\begin{align} \min f(x) \\ \mbox{subject to } \begin{array}{rcl} c_i(x)=0,i \in \mathbf{E} \\ c_i(x)\geq 0, i \in \mathbf{I} \\ \end{array} \end{align}$$這篇文章實作了官網的 同步式 data Parallelism 方法 ref，並且與原本只用一張GPU做個比較。實驗只使用兩張卡，多張卡方法一樣。主要架構如下圖 by TF 官網:
兩張卡等於是把一次要計算的 mini-batch 拆成兩半給兩個 (相同的) models 去並行計算 gradients，然後再交由 cpu 統一更新 model。詳細請自行參考官網。下面直接秀 Codes 和結果。
看了這篇 2017 Microsoft AI and Research 的文章 “Large-Scale Domain Adaptation via Teacher-Student Learning“ 覺得滿有意思的，加上很容易實作，因此就分析一下這篇的可行性。
設計了一個 MNIST Toy Example 來展示 T/S Learning 的能力，自己也想知道這個方法有多可靠。相關的實驗 code 請參考 github
若我們字典裡有 $N$ 個 words, 第 $i$ 個字 $w^i$ 應該怎麼表示呢?
通常使用 one-hot vector 來表示: 把 $w^i$ 變成一個長度 $N$ 的向量 $x^i$。
使用 MNIST and notMNIST 做了一個 AutoEncoder with Fully Connected DNN 的實驗。
依序將實驗結果根據如下步驟顯示出來，程式碼可以參考 [github]
從一開始決定上課後，經過了半年終於來到 Udacity Term2 最後一個 Project 了。只能說盡量讓自己把每一個做的 project 都寫一篇 blog 記錄，但這陣子時間真的不夠用，所以這篇就從 high level 的角度瀏覽一下內容。
記得當年念博的時候，對於SVM頗有愛，也覺得掌握度很高惹，就是 kernel method + convex optimization 的完美合體。直到某天看到 structureSVM，看了老半天實在不得要領，當時就放下沒再管了。多年後 (2015)，剛好台大李宏毅教授教的課程最後一堂 Project demo，有請我們部門介紹做的一些內容給學生，才看到了強大的李老師的課程內容。他所教的 structure learning/svm 實在有夠清楚，又非常 general，真的是強到爆! 本人又年輕，又謙虛，我的新偶像阿!
附上一張我與新偶像的合照… XD
以下內容為筆記用，方便日後回想，來源 大都是李老師的內容。