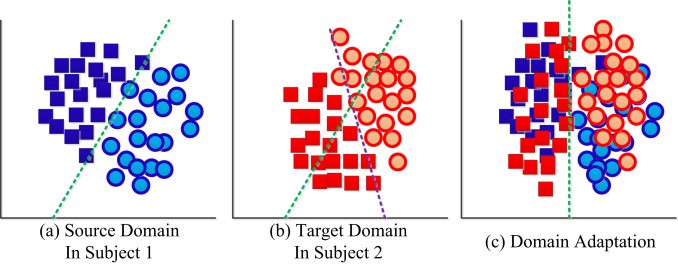
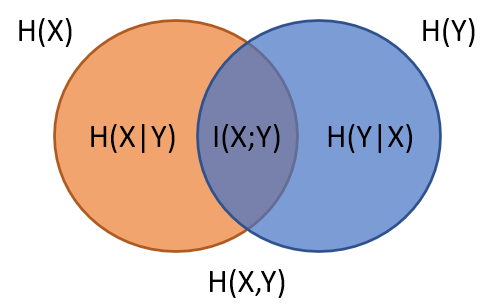
之前聽人介紹 wav2vec [3] 或是看其他人的文章大部分都只有介紹作法, 直到有一天自己去看論文才發現看不懂 CPC [2] (wav2vec 使用 CPC 方法). 因此才決定好好讀一下並記錄.
先將這些方法關係梳理一下, NCE –> CPC (infoNCE) –> wav2vec. 此篇筆記主要紀錄 NCE (Noise Contrastive Estimation)
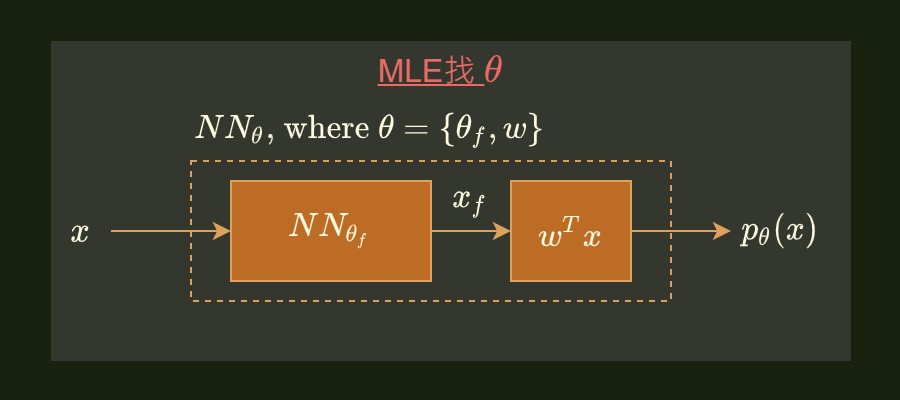
在做 ML 時常常需要估計手上 training data 的 distribution $p_d(x)$. 而我們通常會使用參數 $\theta$, 使得參數的模型跟 $p_d(x)$ 一樣. 在現在 DNN 統治的年代可能會說, 不然就用一個 NN 來訓練吧, 如下圖:
訓練時候的平行化可分為:
由於 Data Parallel 跑同一個完整模型且各 GPU 都用自己複製的一份, 在 update 參數時要如何確保更新一致? 可分為 synchronous 和 asynchronous update. (文章後面會詳細討論)
本文討論 Data Parallel with Synchronous update.
既然要做 data parallel, 第一件事情便是如何對不同 GPU 分派不同的 batches, 接下來我們就使用 PyTorch 做這件事.
NN 在做 quantization 時採用的是非對稱的方式, real ($r$) 和 quantized ($q$) values 對應關係如下:
其中 zero point $Z$ 會跟 $q$ 相同 type, 例如 int8, 而 scaling value $S$ 則會跟 $r$ 相同, 例如 float. 以 uint3 (0~7) 做 quantization, 如下圖所示:
本篇討論以下兩點:
在不同 $Z$/$S$ 轉換有兩個常見理由: 在做 NN 的 quantization 時候, 每個 layer 的 output domain 都不同, 這導致了使用不同的 $Z$/$S$. 又或者丟給 NN 做 inference 之前, mfcc/mfb 需要先轉換到 NN input 的 $Z$/$S$ quantized domain 上.
為了學習 TF2.x 只好把以前練習的一些 projects 重寫一次, 但後來時間斷斷續續的, 所以只做了一部分. 總之先記錄一下目前的練習進度吧.
CTC model 是一個 decoder 部分為簡單的 (independent) linear classifer 的 seq2seq model. 因此 input frame 有 $T$ 個, 就會有 $T$ 個 output distribution vectors.
正常來說 (ex: ASR) output token 數量 $N<T$, 所以會有 alignment 問題. 以往的 alignment (HMM) 強迫每個 frame index 都需對應到一個 phone’s state, 但 CTC 允許對應到 “空” 的 state (null or blank). 這讓 CTC 的 alignment 比 HMM 更有彈性.
RNN-T 是另一種比 CTC 更有彈性的 alignment 表達方式.
CTC 的 gradient 可以非常有效率的用 dynamic programming 求得 (forward/backward 演算法, 下圖). 因此採用 gradient-based optimization 方法就很合適.
本文會詳細介紹上面提到的幾點. Decoding 部分不介紹.
Domain Adaptation 是希望在 source domain 有 label 但是 target domain 無 label 的情況下, 能針對 target domain (或同時也能對 source domain) 進行分類任務. “Adversarial” 的意思是利用 GAN 的 “對抗” 想法: Label predictor 雖然只能保證 source domain 的分類. 但由於我們把 feature 用 GAN 消除了 domain 之間的差異, 因此我們才能期望這時候的 source domain classifier 也能作用在 target domain.
這篇文章 張文彥, 開頭的圖傳達的意思很精確, 請點進去參考.
接著嘗試複現了一次 Domain-Adversarial Training of Neural Networks 的 mnist(source) to mnist_m(target) 的實驗.
說來汗顏, 自從17年三月筆記完 WGAN 後, 就沒再碰 GAN 相關的東西了. 惡補了一下 李宏毅GAN 的課程和其他相關資料, 因此筆記一下.
MMGAN(最原始的GAN), NSGAN(跟MMGAN差別在 G 的 update 目標函式有點不同), f-GAN, WGAN, ADDA (Adversarial Discriminative Domain Adaptation), infoGAN, VAE-GAN 等… 這些全部都是 follow 下面這樣的 framework:
$$\begin{align} Div\left(P_d\|P_G\right) = \max_D\left[ E_{x\sim P_d} D(x) - E_{x\sim P_G}f^*(D(x)) \right] \\ G^*=\arg\min_G{Div\left(P_d\|P_G\right)} + reg(G) \\ \end{align}$$其中 $P_d$ 為 real data pdf, $P_G$ 為 generator 產生的 data pdf. $f^*$ 帶入不同的定義會產生不同的 divergence, 這之後會再說明.
式 (1) 定義了 $P_G$ 與 $P_d$ 的 divergence, 其中這個 divergence 的值為藉由解這個最佳化問題求得的.
式 (2) 表示要找的 $G$ 就是 divergence 最小的那個. Divergence 最小 ($=0$) 同時也表示 $P_G=P_d$ (生成器鍊成). 如果同時考慮 regularization term, $reg(G)$, 則會有很多變化產生, 如 ADDA, infoGAN, VAE-GAN…
我們接著來看 MMGAN, NSGAN, f-GAN, WGAN, ADDA, infoGAN, VAE-GAN 這些怎麼 fit 進這個框架.
整理下 entropy 的一些東西, 不然久沒看老是忘記.
文章會明確定義每一項, 然後在推導它們之間關係的同時會解釋其物理意義.
最後其實就可以整理成類似集合關係的圖 (wiki)
筆記 covariance matrix $R$ 的 determinant 意義以及他的 bound. 這是在讀 Time-delay estimation via linear interpolation and cross correlation 時的 appendix 證明. 覺得有用就筆記下來.
開門見山, $det(R)$ 可以想成 volumn (等於所有 eigenvalues 相乘), 然後 upper bound 就是所有對角項元素相乘.
$$\begin{align} det(R)=\prod_i \lambda_i \leq \prod_i r_{ii} \end{align}$$$\lambda_i$ 是 i-th eingenvalue.
事實上只要 $R$ 是 square matrix, 則 $|det(R)|$ 等於用每個 row vector 做出來的 “平行六面體” 的體積 [ref]
以下筆記論文中證明 $det(R)$ 的 upper bound, 從這個 bound 我們也能看出物理意義.
NN 做分類最後一層通常使用 softmax loss, 但如果類別數量很大會導致計算 softmax 的 cost 太高, 這樣會讓訓練變得很慢. 假如總共的 class 數量是 10000 個, candidate sampling 的想法就是對於一個 input $x$ 採樣出一個 subset (當然需要包含正確的 label), 譬如只用 50 個 classes, 扣掉正確的那個 class, 剩下的 49 個 classes 從 9999 個採樣出來. 然後計算 softmax 只在那 50 個計算. 那麼問題來了, 這樣的採樣方式最終訓練出來的 logits 會是對的嗎? 它與未採樣前 (full set) 的 logtis 有何對應關係?