Credit 是此篇 DingKe ipynb 的, 他完整呈現了 CTC loss 以及 gradient 的計算, 非常棒!
此筆記加入自己的說明, 並且最後使用 tensorflow 來驗證.
這篇另一個主要目的為改成可以練習的格式 (#TODO tag). 因為我相信最好的學習方式是自己造一次輪子, 所以可以的話, 請試著把 #TODO tag 的部分做完吧.
我們只專注在 CTC loss 的 forward, backwark and gradient. Decoding 部分請參考原作者的 ipynb. 最後使用 tf.nn.ctc_loss and tf.gradients 與我們的計算做對比
Variational Inference and VAE Notes
前一陣子學習了 Variational Inference, 因為自己記性只有 LSTM 沒有 L, 所以趕快記下筆記. 學得還是很粗淺, 又是一個大坑阿.
監督學習不外乎就是 training 和 testing (inference). 而 inference 在做的事情就是在計算後驗概率 $p(z|x)$. 在 PGM 中通常是 intractable, 或要找到 exact solution 的計算複雜度太高, 這時 VI 就派上用場了. VI 簡單講就是當 $p(z|x)$ 不容易得到時, 可以幫你找到一個很好的近似, $q(z)$.
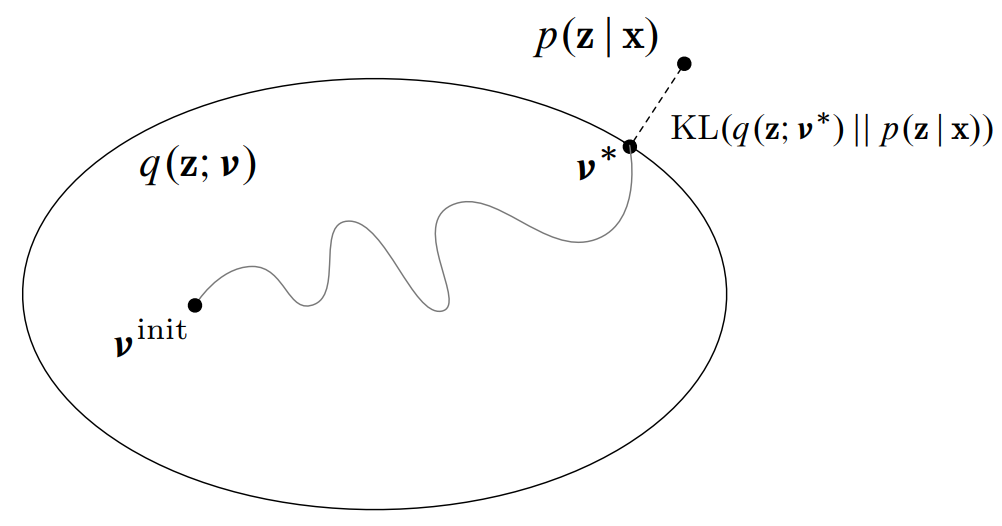
放上一張 NIPS 2016 VI tutorial 的圖, 非常形象地表示 VI 做的事情: 將找 $p(z|x)$ 的問題轉化成一個最佳化問題.
Ensemble Algorithm Summary Notes
這是用自己理解的方式整理了林軒田老師 ML 課程. 其中 Decision tree and Random Forest 沒紀錄.
以前第一次接觸到 Adaboost 的時候就被它深深著迷了, 當時 face detection 可商用算法無不採用經典的 Viola and Jones adaboost method. 在現在 DNN 成主流的時候, 雖然 adaboost 光環已退去, 但在 data mining, data science 領域 boosting 方法仍是最成功的算法之一. 基本上在 Kaggle 比賽可以看到主要兩大方法, 舉凡聲音影像文字等等的辨識就是 DNN, 其他凡是 data mining 相關的就屬 boosting (xgboost).
有趣的是, 近年也有研究人員用 ensemble 的角度看待 DNN, 從這角度就能理解為何一路從 highway network –> skip layer resent –> resnext 的架構演變, 以及為何效果這麼好. 可以參考 “深度神经网络中深度究竟带来了什么?” 很精彩的解釋, 或是 MSR 2017 這篇論文 Deep Convolutional Neural Networks with Merge-and-Run Mappings
筆記內容如下:
TF Notes (5), GRU in Tensorflow
小筆記. Tensorflow 裡實作的 GRU 跟 Colah’s blog 描述的 GRU 有些不太一樣. 所以做了一下 TF 的 GRU 結構. 圖比較醜, 我盡力了… XD
TF 的 GRU 結構

u 可以想成是原來 LSTM 的 forget gate, 而 c 表示要在 memory cell 中需要記住的內容. 這個要記住的內容簡單講是用一個 gate (r) 來控制之前的 state 有多少比例保留, concate input 後做 activation transform 後得到. 可以對照下面 tf source codes.
(what is) Probabilistic Graphical Models
本篇主要介紹什麼是 PGM, 以及一個很重要的應用 Part-of-Speech tagging. PGM 的部分主要圍繞在 “它是什麼?” 也就是 Koller 課程的 Representation. Inference 不討論, 因為自己也沒讀很深入 (汗), 而 Learning 就相當於 ML 裡的 training, 會在介紹 POS 時推導一下.
文章結構如下:
- What is Probabilistic Graphical Model (PGM)?
- What is Bayesian Network (BN)?
- What is Markov Network (MN)? (or Markov Random Field)
- What is Conditional Random Field (CRF)?
- Part-of-Speech (POS) Tagging
- References
文長…
Kaldi Notes (1), I/O in C++ Level
Kaldi I/O C++ Level 筆記, 主要介紹以下幾點, 以及它們在 Kaldi c++ 裡如何關聯:
- 標準 low-level I/O for Kaldi Object
- XXXHolder類別: 一個符合標準 low-level I/O 的類別
- Kaldi Table Object:
<key,value>pairs 組成的 Kaldi 格式檔案 (scp, ark), 其中 value 為 XXXHolder 類別
TF Notes (4), Deconvolution
這篇是個小練習, 就兩點:
- 了解什麼是 deconvolution, 並在 tensorflow 中怎麼用
- 實作一個 CNN AutoEncoder, Encoder 用
conv2d, Decoder 用conv2d_transpose
ROS in Self-driving Car system
這是經歷了漫長的時間, 最後的一哩路了….從2016年12月開始, 到2018年4月中, 花了整整一年五個月. 其實我原先打算半年前就畢業的, 但是中途有狀況, 所以只好 term2 完成後停了半年才開始 term3, 也因此到昨天才剛確定畢業! 而昨天剛好也參加了 Udacity 在中國兩周年的會, 見到了 David Sliver 本人, 算是畢業的一個小紀念!

最後的 project 比較有別於以往, 採用 team work 的方式. 我們的 team 共五人, team lead Franz Pucher 德國, Theodore King 美國, 和我. 疑? 另外兩個呢? 對於 project 完全沒貢獻…我不想說了….= =
Udacity-Semantic-Segmentation
Udacity SDC term 3 第二個 Project 做的是使用 Deep Learning 學習識別 pixel 等級的路面區域. 簡單講就是有如下的 ground truth data, 標示出哪邊是正確的路面, 然後用 Fully Convolutional Network 去對每個 pixel 做識別.


Mixtures of Factor Analyzers
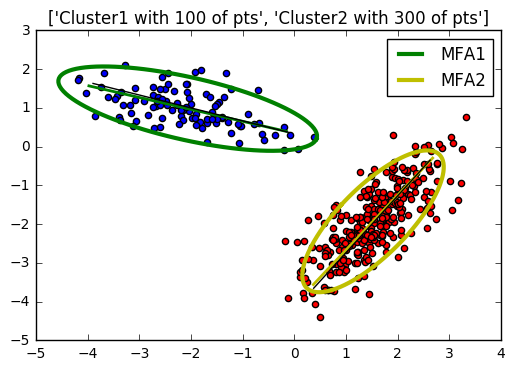
這篇使用 Bishop PRML 的 notations, 同使參考 Zoubin Ghahramani and Geoffrey E. Hinton (沒錯, 就是那位 Hiton, 另外, 第一作者也是神人級別, 劍橋教授, Uber 首席科學家) 1997 年的論文 “The EM Algorithm for Mixtures of Factor Analyzers“, 實作了 Mixtures of Factor Analyzers, 臥槽! 都20年去了! My python implementation, github. 關於 EM 的部分會比較精簡, 想看更多描述推薦直接看 PRML book.
文章主要分三個部分
- 什麼是 Factor Analysis, 以及它的 EM 解
- 推廣到 mixtures models
- 語者識別中很關鍵的 ivector 究竟跟 FA 有什麼關聯?
直接進入正題吧~