Stochastic Processes Week 0 一些預備知識

---

Coursera Stochastic Processes 課程筆記, 共十篇:

• Week 0: 一些預備知識 (本文)
• Week 1: Introduction & Renewal processes
• Week 2: Poisson Processes
• Week3: Markov Chains
• Week 4: Gaussian Processes
• Week 5: Stationarity and Linear filters
• Week 6: Ergodicity, differentiability, continuity
• Week 7: Stochastic integration & Itô formula
• Week 8: Lévy processes
• 整理隨機過程的連續性、微分、積分和Brownian Motion

本篇回顧一些基礎的機率複習, 這些在之後課程裡有用到.
強烈建議閱讀以下文章:

• [測度論] Sigma Algebra 與 Measurable function 簡介
• [機率論] 淺談機率公理 與 基本性質
• A guide to the Lebesgue measure and integration
• Measure theory in probability

以下回顧開始:

---

回顧機率知識

• $e^x=\sum_{k=0}^\infty\frac{x^k}{k!}$. Proof link.

• Independent of Random Variables

  $X\perp Y \Longleftrightarrow \mathcal{P}(XY)=\mathcal{P}(X)\mathcal{P}(Y)$

• $Cov(X,Y)=\mathbb{E}[XY]-\mathbb{E}[X]\mathbb{E}[Y]$
  [Proof]:

  $$Cov(X,Y)=\mathbb{E}[(X-\mu_x)(Y-\mu_y)] \\ =\mathbb{E}[XY]-\mu_x\mathbb{E}[Y]-\mu_y\mathbb{E}[X]+\mu_x\mu_y \\ =\mathbb{E}[XY]-\mu_x\mu_y$$

• $Var(X)=\mathbb{E}[X^2]-(\mathbb{E}[X])^2$
  [Proof]:

  $$Var(X)=Cov(X,X)=\mathbb{E}[XX]-\mathbb{E}[X]\mathbb{E}[X] \\ = \mathbb{E}[X^2]-(\mathbb{E}[X])^2$$

• $X,Y$ uncorrelated $\Longleftrightarrow Cov(X,Y)=0 \Longleftrightarrow \mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]$

• $X\perp Y \Rightarrow$ $X,Y$ uncorrelated $\Rightarrow \mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]$

• Covariance 是線性的: $Cov(aX+bY,cZ)=acCov(X,Z)+bcCov(Y,Z)$
  [Proof]:

  $$Cov(aX+bY,cZ)=\mathbb{E}[(aX+bY)cZ]-\mathbb{E}[aX+bY]\mathbb{E}[cZ] \\ = ac\mathbb{E}[XZ]+bc\mathbb{E}[YZ]-ac\mathbb{E}[X]\mathbb{E}[Z]-bc\mathbb{E}[Y]\mathbb{E}[Z] \\ = ac(\mathbb{E}[XZ]-\mathbb{E}[X]\mathbb{E}[Z])+bc(\mathbb{E}[YZ]-\mathbb{E}[Y]\mathbb{E}[Z]) \\ = acCov(X,Z)+bcCov(Y,Z)$$

• [Characteristic Function Def]:
  For random variable $\xi$, 定義 characteristic function $\Phi:\mathbb{R}\rightarrow \mathbb{C}$ 為
  

  $$\Phi_\xi(u) = \mathbb{E}\left[ e^{iu\xi} \right]$$

• 如果 $\xi_1\perp\xi_2$, 則

  $\Phi_{\xi_1+\xi_2}(u)=\Phi_{\xi_1}(u)\Phi_{\xi_2}(u)$

  [Proof]:

  $$\Phi_{\xi_1+\xi_2}(u)=\mathbb{E}[e^{iu(\xi_1+\xi_2)}]=\mathbb{E}[e^{iu\xi_1}e^{iu\xi_2}] \\ = \int_{\xi_1,\xi_2} \mathcal{P}(\xi_1,\xi_2)e^{iu\xi_1}e^{iu\xi_2} d\xi_1 d\xi_2 \\ = \int_{\xi_1,\xi_2} \left(\mathcal{P}(\xi_1)e^{iu\xi_1}\right)\left(\mathcal{P}(\xi_2)e^{iu\xi_2}\right) d\xi_1 d\xi_2 \\ =\mathbb{E}[e^{iu\xi_1}]\mathbb{E}[e^{iu\xi_2}] \\ =\Phi_{\xi_1}(u)\Phi_{\xi_2}(u)$$

• $\mathbb{E}[X+Y]=\mathbb{E}[X]+\mathbb{E}[Y]$. 跟 $X,Y$ 是否獨立或不相關無關.

• $|Cov(X,Y)|\leq\sqrt{Var(X)}\sqrt{Var(Y)}$
  [Proof]: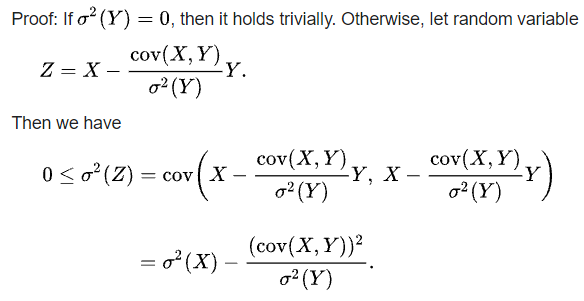
  

• $Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$
  [Proof]:

  $$Var(X+Y)=Cov(X+Y,X+Y)\\ =Cov(X,X)+2Cov(X,Y)+Cov(Y,Y)\\ =Var(X)+Var(Y)+2Cov(X,Y)$$

• 如果 $X,Y$ uncorrelated (所以 $X\perp Y$ 也成立), 則 $Var(X+Y)=Var(X)+Var(Y)$

• Normal distribution of one r.v.

  $$X\sim\mathcal{N}(\mu,\sigma^2), \text{ for }\sigma>0,\mu\in\mathbb{R} \\ p(x)=\frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

• The characteristic function of normal distribution is:

  $\Phi(u)=e^{iu\mu-\frac{1}{2}u^2\sigma^2}$

• 獨立高斯分佈之和仍為高斯分佈, mean and variance 都相加
  [Proof]:

  $(X_1,...,X_n) \text{ where } X_k\sim\mathcal{N}(\mu_k,\sigma_k^2),\forall k=1,...,n$

  我們知道

  $$X_k\sim\mathcal{N}(\mu_k,\sigma_k^2)\longleftrightarrow \Phi_k(u)=e^{iu\mu_k-\frac{1}{2}u^2\sigma_k^2}$$

  則

  $$\sum_k X_k \longleftrightarrow \prod_k \Phi_k(u) = e^{iu(\sum_k \mu_k)-\frac{1}{2}u^2(\sum_k \sigma_k^2)}$$

  由特徵方程式與機率分佈一對一對應得知

  $\sum_k X_k \sim \mathcal{N}\left(\sum_k \mu_k, \sum_k \sigma_k^2\right)$

• $K:\mathcal{X}\times\mathcal{X}\rightarrow\mathbb{R}$ is symmetric positive semi-definite:
  

• 給定 $t_1<t_2<…<t_n$ 一個很有用的技巧為:
  可以變成以下這些 disjoint 區段的線性組合

  $(t_2-t_1),...,(t_n-t_{n-1})$

  具體如下:

  $$\sum_{k=1}^n \lambda_k B_{t_k} = \lambda_n(B_{t_n}-B_{t_{n-1}}) + (\lambda_n+\lambda_{n-1})B_{t_{n-1}} + \sum_{k=1}^{n-2} \lambda_k B_{t_k} \\ = \sum_{k=1}^n d_k(B_{t_n}-B_{t_{n-1}})$$

  會想要這樣轉換是因為課程會學到 independent increment 特性, 表明 disjoint 區段的 random variables 之間互相獨立, 因此可以變成互相獨立的 r.v.s 線性相加

• Calculating Moments with Characteristic Functions (wiki))
  

• Brownian Motion reference
  Brownian Motion by Hartmann.pdf

• Lebesgue Measure and Integration
  A guide to the Lebesgue measure and integration
  Lebesgue integration from wiki
  [測度論] Sigma Algebra 與 Measurable function 簡介

• Probability Theory
  [機率論] 淺談機率公理 與 基本性質
  Measure theory in probability
  Distribution function $F$ defined with (probability) measure $\mu$ (ref)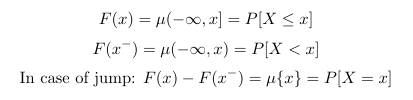
  
  $F$ 又稱 cumulative distribution function (c.d.f.), 或稱 cumulative function
  其微分稱為 probability density function (p.d.f.), 或簡稱 density function. 注意到 density 不是 (probability) measure $\mu$!
  而期望值可以用 Lebesgue measure or in probability measure 來看待:
  Given Probability space: $(\Omega,\Sigma,\mathcal{P})$, 期望值定義為
  

  所有 event $\omega\in\Sigma$ 的 probability measure $\mathcal{P}(\omega)$, 乘上該 random variable 的值 $X(\omega)$
  所有 outcome $\omega\in\Omega$ 的 probability measure $\mathcal{P}(d\omega)$, 乘上該 random variable 的值 $X(\omega)$

• Lebesgue’s Dominated Convergence Theorem: Exchanging $\lim$ and $\int$
  Let $(f_n)$ be a sequence of measurable functions on a measure space $(S,\Sigma,\mu)$. Assume $(f_n)$ converges pointwise to $f$ and is dominated by some (Lebesgue) integrable function $g$, i.e.

  $|f_n(x)|\leq g(x), \qquad \forall n,\forall x\in S$

  Then $f$ is (Lebesgue) integrable, i.e. $\int_S |f|d\mu<\infty$
  and

  $$\lim_{n\rightarrow\infty}\int_S |f_n-f|d\mu=0 \\ \lim_{n\rightarrow\infty}\int_S f_nd\mu = \int_S\lim_{n\rightarrow\infty}f_nd\mu = \int_S f d\mu$$