這是一篇論文筆記: “Estimation of Non-Normalized Statistical Models by Score Matching”, 其實推薦直接讀論文, 數學式很清楚, 表達也明確, 只是想順著自己的說法做一下筆記
動機介紹
在 Machine Learning 中, 我們常常希望用參數 $\theta$ 估出來的 pdf $p(.;\theta)$ 能跟真實 data (training data) 的 pdf $p_x(.)$ 愈像愈好.
由於是 pdf $p(.;\theta)$, 必須滿足機率形式, i.e. 積分所有 outcomes 等於 1, 因此引入一個 normalization term $Z(\theta)$
$$p(\xi;\theta)=\frac{1}{Z(\theta)}q(\xi;\theta)$$
其中 $\xi\in\mathbb{R}^n$ 為一個 data point
假設我們有 $T$ 個 observations $\{x_1,...,x_T\}$, 套用 empirical expecation 並對 likelihood estimation 找出最佳 $\theta$ (MLE):
$$\theta_{mle}=\arg\max_\theta \sum_{t=1}^T \log p(x_t;\theta)$$
計算 gradient, 會發現由於存在 $Z(\theta)$ 變得很難計算, 導致 gradient-based optimization 也很困難.
山不轉路轉, 如果我們能換個想法:
不要求找到的 $\theta$ 對每個 data points $x_t$ 使其 $p(x_t;\theta)$ 跟真實機率分佈的結果很接近, i.e. $p(x_t;\theta)\approx p_x(x_t)$
改成希望使其
$$\begin{align}
\nabla_x\log p_x(x_t) \approx
\nabla_x\log p(x_t;\theta)
{\color{orange}{=\nabla_x\log q(x_t;\theta)}}
\end{align}$$
意思是希望每個 data points 他們的 (log) gradient 都跟真實分布的 (log) gradient 接近
可以想像兩個 functions 的變化一致的話, 它們的長相應該會很接近 (只差在scale不同)
以下圖舉例來說 (該圖引用自 Yang Song: Generative Modeling by Estimating Gradients of the Data Distribution), vector field 箭號表示那些 (log) gradients, 而 contours 表示一個 mixture of two Gaussians
我們要求 vector field 一致
藉由這樣找 $\theta$ 的方法, 我們其實找到的是 non-normalized distribution $q(.;\theta)$.
直觀的 Objective Function (Explicit Score Matching)
我們使用 MSE loss 來計算式 (1), 利用此 loss 找最佳 $\theta$ 的方法稱為 Score Matching
定義 score function, 它其實就是 gradient of the log-density with respect to the data vector:
- Data pdf 的 score function: $\psi_x(\xi)=\nabla_\xi\log p_x(\xi) \in \mathbb{R}^n$
- Model pdf 的 score function: $$\psi(\xi;\theta)= \left( \begin{array}{c} \frac{\partial\log p(\xi;\theta)}{\partial\xi_1} \\ \vdots\\ \frac{\partial\log p(\xi;\theta)}{\partial\xi_n} \end{array} \right) =\left( \begin{array}{c} \psi_1(\xi;\theta) \\ \vdots \\ \psi_n(\xi;\theta) \end{array} \right) = \nabla_\xi\log p(\xi;\theta) =\color{orange}{\nabla_\xi\log q(\xi;\theta)}$$
因此 objective function 就是這兩個 score functions 的 MSE (又稱為 Fisher Divergence: Interpretation and Generalization of Score Matching):
$$\begin{align}
J(\theta)=\frac{1}{2}\int_{\xi\in\mathbb{R}^n} p_x(\xi) \| \psi(\xi;\theta)-\psi_x(\xi) \|^2 d\xi
\end{align}$$
而 score matching estimator 的參數就是
$$\hat{\theta}=\arg\min_\theta J(\theta)$$
要算期望值需要知道真實資料的 pdf $p_x(.)$, 雖然我們無法得到, 但可以根據 training data 去計算 empirical 期望值.
例如我們有 $T$ 個 observations $\{x_1,...,x_T\}$, 則 empirical expectation 為
$$\tilde{J}(\theta)=\frac{1}{T}\sum_{t=1}^T \| \psi(x_t;\theta) - \psi(x_t) \|^2$$
不過 (2) 最麻煩的是我們不知道真實資料的 score function $\psi_x(.)$, 論文的定理說明了在某些簡單的條件下, 可以避免掉計算這項.
條件為: 除了 pdf 可微, 1st/2nd moment 存在, 一個比較特殊的條件為 (但也容易滿足):
$$p_x(\xi)\psi(\xi;\theta)\xrightarrow[\|\xi\|\rightarrow \infty]{}0$$
我們在下面會看出來
Practical Objective Function (Implicit Score Matching)

擷自論文. 將 Appendix 的證明描述如下:
將 (2) 展開變成
$$J(\theta)=\int p_x(\xi)\left[
\frac{1}{2}\|\psi_x(\xi)\|^2 + \frac{1}{2}\|\psi(\xi;\theta)\|^2 - \psi_x(\xi)^T\psi(\xi;\theta)
\right] d\xi \\
=\int p_x(\xi)\left[
\frac{1}{2}\|\psi(\xi;\theta)\|^2
{\color{orange}
{- \psi_x(\xi)^T\psi(\xi;\theta)}}
\right]d\xi + const$$
將向量的內積展開, 改寫橘色部分積分如下:
$$-\sum_{i=1}^n \int p_x(\xi)\psi_{x,i}(\xi)\psi_i(\xi;\theta)d\xi \\
\text{by def. of score function }= -\sum_{i=1}^n \int p_x(\xi) \frac{\partial \log p_x(\xi)}{\partial \xi_i} \psi_i(\xi;\theta) d\xi \\
= -\sum_{i=1}^n \int \frac{p_x(\xi)}{p_x(\xi)} \frac{\partial p_x(\xi)}{\partial \xi_i} \psi_i(\xi;\theta) d\xi = \sum_{i=1}^n
{\color{green}{
-\int \frac{\partial p_x(\xi)}{\partial \xi_i} \psi_i(\xi;\theta) d\xi}}$$
使用分部積分 (為簡化notation, 只看第一維的變數 $\xi_1$)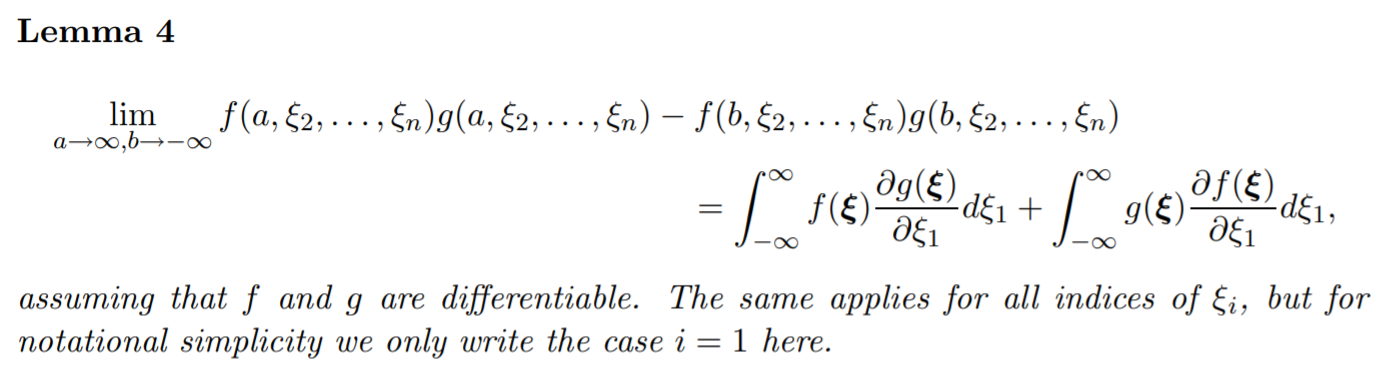
改寫綠色部分變成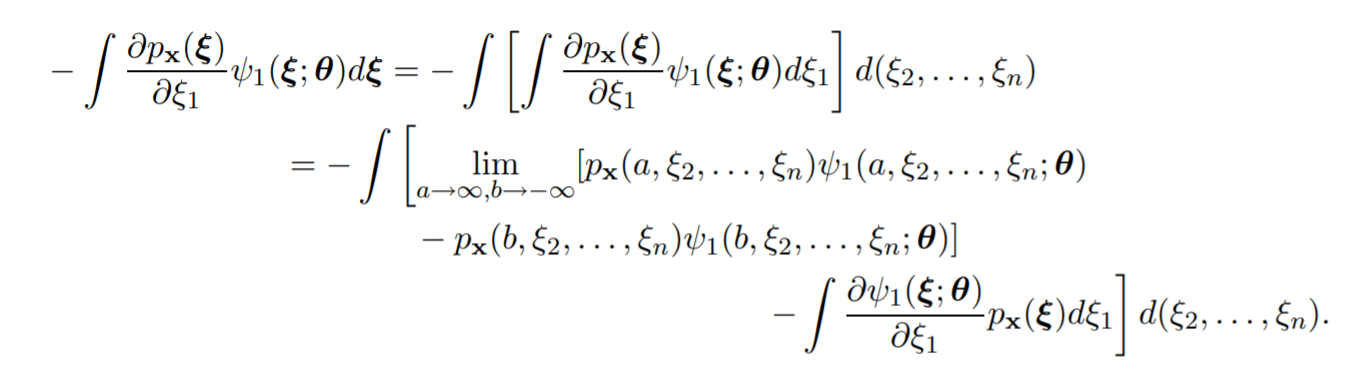
只要假設
$$p_x(\xi)\psi(\xi;\theta)\xrightarrow[\|\xi\|\rightarrow \infty]{}0$$
則最後只剩下
$$-\int\frac{\partial p_x(\xi)}{\partial\xi_i}\psi_i(\xi;\theta)d\xi = \int\frac{\partial\psi_i(\xi;\theta)}{\partial\xi_i}p_x(\xi)d\xi$$
將此結果一路代回去 (需要一點耐心而以), 就可以得到式 (3) 了, 重複一下式 (3) 如下:
$$\begin{align}
J(\theta)=\int_{\xi\in\mathbb{R}^n}p_x(\xi)\sum_{i=1}^n\left[
\partial_i\psi_i(\xi;\theta)+\frac{1}{2}\psi_i(\xi;\theta)^2
\right]d\xi + const
\end{align}$$
Optimize 這個目標函式就容易得多了, 只要使用 empirical expecation 就可以:
$$\begin{align}
\tilde{J}(\theta)=\frac{1}{T}\sum_{t=1}^T\sum_{i=1}^n\left[
\partial_i\psi_i(x_t;\theta)+\frac{1}{2}\psi_i(x_t;\theta)^2
\right] + const
\end{align}$$
最佳解的存在唯一性

證明:
對照式 (2) 的目標函數:
$$\begin{align}
J(\theta)=\frac{1}{2}\int_{\xi\in\mathbb{R}^n} p_x(\xi) \| \psi(\xi;\theta)-\psi_x(\xi) \|^2 d\xi
\end{align}$$
只要我們的 parameter space 夠大能夠包含真實的 pdf, 當目標函式達到最小, i.e. $=0$, 則解就是真實的 pdf
討論
總結最後的 objective function:
$$J(\theta)=\int_{\xi\in\mathbb{R}^n}p_x(\xi)\sum_{i=1}^n\left[
\partial_i\psi_i(\xi;\theta)+\frac{1}{2}\psi_i(\xi;\theta)^2
\right]d\xi$$
簡化改寫一下
$$\begin{align}
J(\theta)=\mathbb{E}_{p_x(\xi)}\left[
tr(\nabla_\xi\psi(\xi;\theta))+\frac{1}{2}\|\psi(\xi;\theta)\|_2^2
\right]
\end{align}$$
其中 $\psi(\xi;\theta):\mathbb{R}^n\rightarrow \mathbb{R}^n$, 實務上我們就用一個 NN 參數為 $\theta$ 表示, 因此原本需要二階導數, 變成只需要一階導數在 loss 中. 雖然這樣做比較有效率, 但 Deep Energy Estimator Networks 指出會不 robust.
後續在這篇文章 “A Connection Between Score Matching and Denoising Autoencoders”, 作者提出 Denoising Score Matching (DSM) 目標函式, 可以不需要將 gradient 也納入 loss 中.
其想法就是將每個 data $x$ 根據 Gaussian pdf 做些擾動, 所以一個副作用是永遠學不到最準的 data pdf (除非沒有擾動), 但可藉由加入的擾動愈小, 讓估計愈真實
Score matching 的作法是 2005 年, 而作者 Aapo Hyv¨arinen 其實也是 Noise Contrastive Estimation (NCE) 的作者. (參考之前的 NCE 筆記)
NCE 也是在做一樣的事情: 想辦法避開 $Z(\theta)$ 來估計真實資料的 pdf. 但發表在 2010 年.
這一問題, probabilistic model flexibility 與 tractability 的 trade-off, 在 Machine Learning 是被探討很久的問題, 這篇 Deep Unsupervised Learning using Nonequilibrium Thermodynamics, (Diffusion Probabilistic Model 開始的重要文章) 的 introduction 描述一些主要方法, 可以盡量滿足 flexibility 情況下, 又能 tractable.
Score matching 可以應用在 Langevin dynamics, 透過只使用 score function $\nabla_x\log p(x)$ 就可以用 MCMC 取 samples, 而這一步驟在 Diffusion Probabilistic Model 中扮演著重要的角色
同時 NCE 在 Self-supervised Learning 同樣也是關鍵, 衍生了 infoNCE, CPC, … 這一派的 SSL 方法
👏真神人也👏
