這是一篇論文筆記: “A Connection Between Score Matching and Denoising Autoencoders”
建議看本文前請先參前一篇: Score Matching 系列 (一) Non-normalized 模型估計
前言
基於 Score Matching, 提出 Denoising Score Matching (DSM) 的目標函式, 好處是在 energy-based model 下:
- 不用將 score function 的 gradients 也納入 loss 去計算 (避免二次微分做 backprop 提高效率)
- 當 input $x$ 的維度很大也沒問題 (可以 scalable)
但缺點是:
- 最多只能學到加 noise 後的分布
- 加 noise 的 level 不好調整
這兩個缺點在下一篇 Sliced Score Matching (SSM) 可以得到改善
這篇論文最後也點出了 denoising autoencoder 跟 score matching 的關係 (實際上就是 DSM loss)
正文
$q(x)$ 表示 data (真實資料) 的 pdf, $p(x;\theta)$ 表示 model 參數為 $\theta$ 的 pdf
Explicit Score Matching (ESM) 為:
$$\begin{align}
J_{ESM,q}(\theta) = \mathbb{E}_{q(x)}\left[
\frac{1}{2}\left\|
\psi(x;\theta)-\frac{\partial \log q(x)}{\partial x}
\right\|^2
\right]
\end{align}$$
實際上我們不知道 $q(x)$, 因此式 (1) 的 $J_{ESM}$ 我們無法用. 不過, 最開始的 Score Matching 論文已經證明 $J_{ESM}$ 等價於如下的 $J_{ISM}$, 而 $J_{ISM}$ 是我們能實作的
Implicit Score Matching (ISM) 為:
$$\begin{align}
J_{ISM,q}(\theta)=\mathbb{E}_{q(x)}\left[
\frac{1}{2}\|\psi(x;\theta)\|^2+ tr(\nabla_x\psi(x;\theta))
\right]
\end{align}$$
如果我們對 $q(x)$ 做 pertrub, i.e. 每一個 data point $x$ 都加上一個 pdf 為 $q_\sigma(\tilde{x}|x)$ 的 random noise
其中 $\sigma$ 為該 noise pdf 的參數, 如果以 isotropic Gaussian pdf 為例子, $\sigma^2$ 就是 variance
則 noisy 的 data pdf $q_\sigma(\tilde{x})$ 就變成:
$q_\sigma(\tilde{x})=\int q_\sigma(\tilde{x}|x) q(x) dx$
💡 兩個 independent random variables $x,y$ 相加 $z=x+y$, 則 $z$ 的 pdf 為 $x,y$ 的 pdfs 的 convolution
然後 $\theta$ 要學的目標 pdf 變成 $q_\sigma(\tilde{x})$ 後, 其 ESM 為:
$$\begin{align}
J_{ESM,q_\sigma}(\theta) = \mathbb{E}_{q_\sigma(\tilde{x})}\left[
\frac{1}{2}\left\|
\psi(\tilde{x};\theta)-\frac{\partial \log q_\sigma(\tilde{x})}{\partial \tilde{x}}
\right\|^2
\right]
\end{align}$$
只是將原來的 ESM data pdf 換成 noisy 版本而已. 因此, $J_{ESM,q_\sigma}$ 也會等價 $J_{ISM,q_\sigma}$ (只要適當的 noise pdf 讓 $q_\sigma(\tilde{x})$ 滿足原來 ESM 等於 ISM 的條件)
其中:
$$\begin{align}
J_{ISM,q_\sigma}(\theta)=\mathbb{E}_{q_\sigma(\tilde{x})}\left[
\frac{1}{2}\|\psi(\tilde{x};\theta)\|^2+ tr(\nabla_x\psi(\tilde{x};\theta))
\right]
\end{align}$$
⚠️ 乍看之下 (4) 好像跟原來的 ISM (式 (2)) 沒什麼不同, 其實不同的地方在 “expectation on what pdf”
ISM 的缺點是必須要計算二次微分, 並且要當成 loss 的一部分, 這會導致計算過慢 (因為微分的 operations 也會加進 graph 裡, 可以想像 NN 本來的 graph 就很大了, 還要加一二次微分的 ops 進去)
- 有關如何將一二次微分加入 loss 中可參考 [retain_graph和create_graph参数]
- 其實我們可以直接用一個 NN 來表示 score function $\psi(x;\theta)$, 這樣原來的二次微分就是該 NN 的一次微分, 雖然這樣做比較有效率, 但 Deep Energy Estimator Networks 指出會不 robust. 不過如果使用 Sliced Score Matching (SSM), 該文作者說一樣可以有效的用 NN 直接 predict score function.
這篇論文提出的 Denoising Score Matching (DSM) 的目標函式 $J_{DSM,q_\sigma}(\theta)$ 可以避開上述將微分項也加入 loss 計算導致不有效率的缺點. 該目標函式為:
$$\begin{align}
J_{DSM,q_\sigma}(\theta)=\mathbb{E}_{q_\sigma(x,\tilde{x})}\left[
\frac{1}{2}
\left\|
\psi(\tilde{x};\theta) - \frac{\partial\log q_\sigma(\tilde{x}|x)}{\partial\tilde{x}}
\right\|^2
\right]
\end{align}$$
注意到若 noise pdf 為 isotropic Gaussian nosie $\mathcal{N}(x,\sigma^2I)$ 則:
因此式 (5) 變得很容易計算也有效率
💡 還有一個直觀的解釋, 我們給定一個 pair $(x,\tilde{x})$, 希望 $\tilde{x}$ 的 gradient 跟 noise pdf 的 gradient 流向一樣, 相當於希望將 nosiey 的 $\tilde{x}$ 還原成 clean 的 $x$
文章並證明了 $J_{DSM_{q_\sigma}}$ 等價於 $J_{ESM_{q_\sigma}}$, i.e. (5)=(3)
我們擷取論文 Appendix 的證明: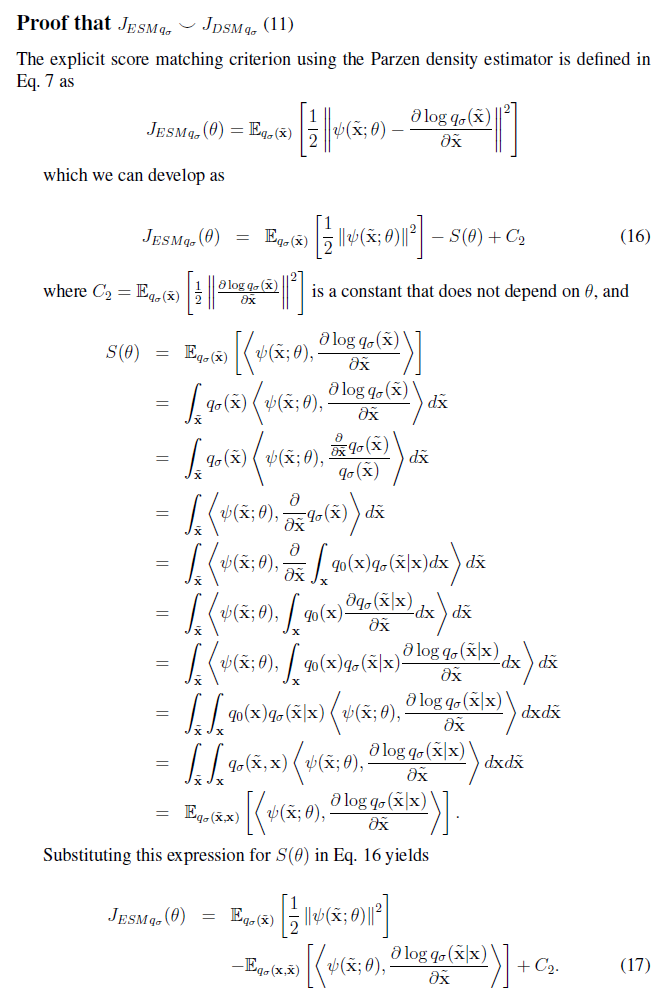

最後文章說明了一個有趣的發現
最簡單的 Denoise Autoencoder NN (一層 linear hidden layer, tied weights) 其 reconstruction mse 的目標函式等價於使用 $J_{DSM_{q_\sigma}}$
讓我們將 Score Matching 跟 Denoise Autoencoder 有了連結