這是一篇論文筆記: “Sliced-Score-Matching-A-Scalable-Approach-to-Density-and-Score-Estimation”
建議看本文前請先參前兩篇: Score Matching 系列 (一) 和 Score Matching 系列 (二)
雖然 DSM (文章在系列二) 比起 SM 可以非常有效率的訓練, 但最多只能還原到 noisy 的分布, 且加噪的強度不易調整.
本篇 SSM or SSM-VR 則不會有此缺點, 且效果可以接近原來的 SM.
背景回顧
真實資料的 pdf $p_d(x)$ 和其 score function 定義如下:
$$s_d(x) \triangleq \nabla_x \log p_d(x)$$
Model 的 non-normalized density $\tilde{p}_m(x;\theta)$ 和 pdf $p(x;\theta)$ 以及 score function 定義如下:
$$p_m(x;\theta)=\frac{\tilde{p}_m(x;\theta)}{Z_\theta}, \\
s_m(x;\theta) \triangleq \nabla_x\log p_m(x;\theta) = \nabla_x\log \tilde{p}_m(x;\theta)$$
最原始的 loss function (Fisher divergence), 或在我們前面的文章稱 Explicit Score Matching (ESM):
$$\begin{align}
L(\theta) \triangleq \frac{1}{2}\mathbb{E}_{p_d}\left[
\| s_m(x;\theta) - s_d(x) \|_2^2
\right]
\end{align}$$
其中式 (1) 等價於下式的 Implicit Score Matching (ISM) 的目標函式:
$$\begin{align}
J(\theta)=\mathbb{E}_{p_d}\left[
tr(\nabla_x s_m(x;\theta))+\frac{1}{2}\|s_m(x;\theta)\|_2^2
\right]
\end{align}$$
雖然 ISM 可以計算, 但需要用到二次微分, 當 network 參數量大的時候, Hessian matrix 效率很低. 同時 $x$ 維度高的時候效率也是很低 (無法很好 scalable)
為此, 上一篇 DSM 利用加入 noise 的方式避掉這兩個問題, 但有兩個缺點
- 最多只能學到加噪聲的分布
- noise 的 level, i.e. $\sigma^2$, 很難調
SSM(-VR) 能改善這兩個缺點
Sliced Score Matching (SSM)
本篇 sliced score matching 則利用另一種想法, 不在高維度的 score function 上比較, 而是將 score function randomly 投影在低維度上再比較, 因此目標函式從 (1) 變成下式:
$$\begin{align}
L(\theta;p_v)\triangleq \frac{1}{2}\mathbb{E}_{p_v}\mathbb{E}_{p_d}\left[
\left( v^T s_m(x;\theta) - v^T s_d(x) \right)^2
\right]
\end{align}$$
其中 $v$ 是 random direction, $v \sim p_v$, $x\sim p_d$ are independent, 同時要求
$$\mathbb{E}_{p_v}[vv^T] \succ 0, \mathbb{E}_{p_v}[\|v\|_2^2]<\infty$$
如同 ESM 推導成等價的 ISM (式 (1) 到 (2) 去掉 $s_d$), (3) 也可以將 $s_d$ 去掉:
$$\begin{align}
J(\theta;p_v) \triangleq \mathbb{E}_{p_v}\mathbb{E}_{p_d} \left[
v^T\nabla_x s_m(x;\theta)v + \frac{1}{2}(v^Ts_m(x;\theta))^2
\right]
\end{align}$$
基本上對每個 sample 出來的 $x_i$, 我們都可以 sample 出 $M$ 個投影向量, 所以 empirical expecation 寫法如下:
$$\begin{align}
\hat{J}(\theta)\triangleq \frac{1}{N}\frac{1}{M}\sum_{i=1}^N\sum_{j=1}^M v_{ij}^T\nabla_x s_m(x_i;\theta)v_{ij} + \frac{1}{2}(v_{ij}^T s_m(x_i;\theta))^2
\end{align}$$
同時如果 $p_v$ 是 multivariate standard normal or Rademacher distribution, 則可以簡化為:
$$\begin{align}
\hat{J}_{vr}(\theta)\triangleq \frac{1}{N}\frac{1}{M}\sum_{i=1}^N\sum_{j=1}^M v_{ij}^T\nabla_x s_m(x_i;\theta)v_{ij} + \frac{1}{2}\|s_m(x_i;\theta)\|_2^2
\end{align}$$
稱為 Sliced Score Matching with Variance Reduction (SSM-VR)
文章說 SSM-VR 比 SSM 表現更好, 同時投影向量的數量, $M$, 選擇 1 個就很好了
看到這可能還是有疑問, 看起來還是得算 Hessian matrix, $\nabla_x s_m(x;\theta)$, 阿? 不是說要可以加速有效率?
其實是這樣的, 先算 $v^T s_m(x;\theta)$ 對 $x$ 的微分, 由於是 scalar 的 backprob 就快很多, 因此得到 $v^T\nabla_x s_m(x;\theta)$, 然後再跟 $v$ 內積就結束了
因此算法如下
Codes 可以參考 https://github.com/Ending2015a/toy_gradlogp/blob/master/toy_gradlogp/energy.py#L152
實驗
論文裡一段實驗結果如下: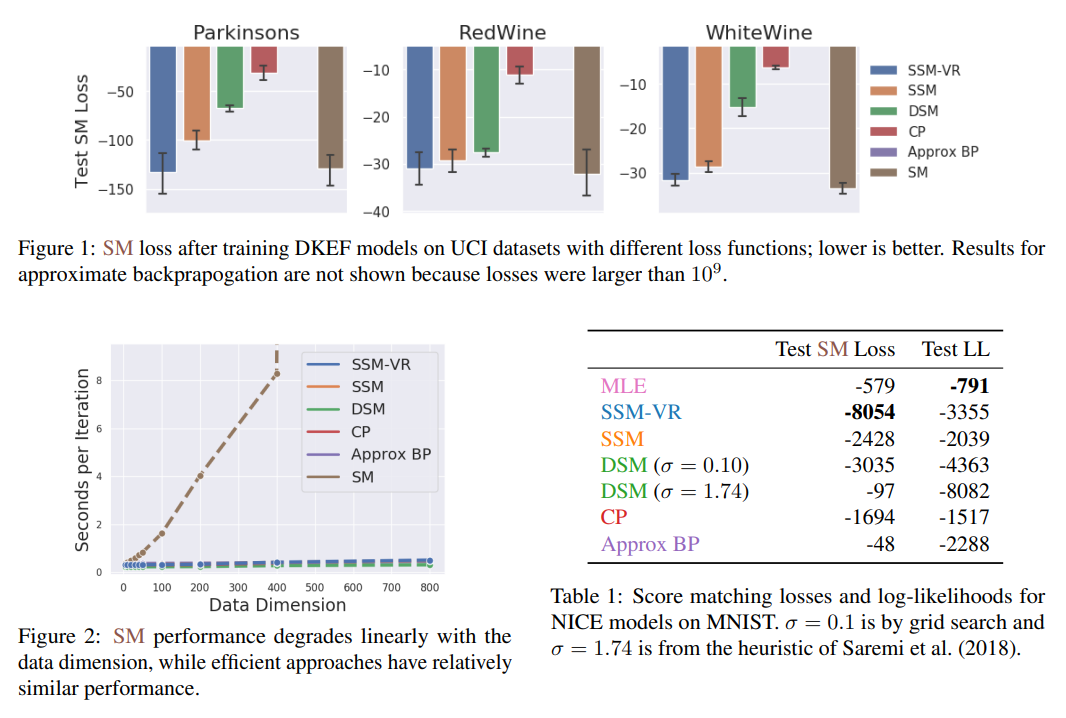
SM loss 指的是式 (1) 的 loss, SM 算法則是式 (2) Implicit Score Matching (ISM)
DSM 指的是 Denosing Score Matching. 先忽略 CP 和 Approx BP (因為我沒看 XD)
從 Figure 1 可以看出 SSM(-VR) 的 performance 可以達到跟 SM 接近, 也比 DSM 好上一截.
而 Figure 2 可以看出 SSM(-VR) 的 scalibility (DSM 也很有效率), 這是原來的 SM 達不到的 (因為要算 Hessian)
Table 1 也可以看出 DSM 對於 noise 的強度 ($\sigma$) 較敏感.
總之, SSM(-VR) 可以跟 DSM 一樣 scalable 和 efficient, 且 performance 比 DSM 好又接近原來的 SM.
另外提一下這篇的作者, Yang Song, 對於 score matching 以及後來的 diffusion probabilistic model 都有很重要的著作和進展, 值得讀他的論文 👏