忘記物理也要搞懂的 Hamiltonian Monte Carlo (HMC) 筆記

先說我物理什麼的都還給老師了, 只能用自己理解的方式, 筆記下 Hamiltonian dynamic.

　💡 如果連我都能懂, 相信大家都能理解 HMC 了

但還是建議先看 MCMC by Gibbs and Metropolis-Hasting Sampling, 因為這篇要說的 Hamiltonian Monte Carlo (HMC) 是 Metropolis-Hastings (MH) 方法的一種, 只是 proposal distribution 從 random walk 改成使用 Hamiltonian dynamics 來做, 因而變的非常有效率 (accept rate 很高), 且對於高維度資料採樣也很有效.

首先粗體字如 $\mathbf{x}, \mathbf{v}, \mathbf{p}$ 都是 column vector, 而非粗體字表 scalar, e.g. $m,t$

Hamiltonian dynamic

一物體在位置 $\mathbf{x}$ (這裡可想成是高度) 的重力位能 (potential energy) 為

$$\begin{align} U(\mathbf{x})=m\mathbf{g}^T\mathbf{x} \end{align}$$

其中 $m$ 表質量, $\mathbf{g}$ 表重力加速度 (是個向量, 所以有方向性).
同時該物體, 其本身也存在動能 (kinetic energy) 且可表示為:

$$\begin{align} K(\mathbf{p})=\frac{\mathbf{p}^T\mathbf{p}}{2m}\left(=\frac{1}{2}m\mathbf{v}^2\right) \\ \mathbf{p}=m\frac{d\mathbf{x}}{dt}\left(=m\mathbf{v}\right) \end{align}$$

$\mathbf{v}$ 表速度 (是個向量, 所以有方向性), $\mathbf{p}$ 我們稱為動量 (momentum).
整個封閉系統 (沒有外界的其他能量介入) 的能量為:

$$\begin{align} H(\mathbf{x},\mathbf{p})=U(\mathbf{x})+K(\mathbf{p}) \\ =m\mathbf{g}^T\mathbf{x}+\frac{\mathbf{p}^T\mathbf{p}}{2m} \end{align}$$

根據能量守恆 (energy conservation), 不管時間 $t$ 是什麼, 整個系統的能量 $H(\mathbf{x},\mathbf{p})$ 都維持相同.
此時如果我們知道該物體的初始狀態 $(\mathbf{x}_0,\mathbf{p}_0)$ 的話, 事實上可以知道任何時間 $t$ 下的位置和動量 $(\mathbf{x},\mathbf{p})$
而這樣的關係可以由下面的 Hamiltonian equations 描述出來:

$$\begin{align} \frac{dx_i}{dt}=\frac{\partial H}{\partial p_i} \\ \frac{dp_i}{dt}=-\frac{\partial H}{\partial x_i} \end{align}$$

其中 $i\in\{1,..,d\}$, $d$ 表空間的維度.

只要使用 $\mathbf{p}=m\mathbf{v}$, 速度 $\mathbf{v}$ 是 $\mathbf{x}$ 對時間的微分, 以及
速度對時間的微分等於負加速度 $-\mathbf{g}$ (座標系統定義為往上的座標是正的, 而重力加速度是向下的, 所以值為負)
就可以從 (5) 推導出 (6) 和 (7).
$$\frac{\partial H}{\partial p_i}=\frac{\partial K(\mathbf{p})}{\partial p_i}=\frac{\partial}{\partial p_i}\frac{\sum_j p_j^2}{2m}=\frac{p_i}{m}=\frac{m v_i}{m}=v_i=\frac{dx_i}{dt} \\ \frac{\partial H}{\partial x_i}=\frac{\partial U(\mathbf{x})}{\partial x_i}=\frac{\partial m\sum_j g_jx_j}{\partial x_i}=mg_i=m\frac{d(-v_i)}{dt}=-\frac{dmv_i}{dt}=-\frac{dp_i}{dt}$$

所以如果已知時間 $t$ 的位置 $x_i(t)$, 想預估 $t+\varepsilon$ 的位置 $x_i(t+\varepsilon)$ 的話, 可以透過 (6) 的方式更新:

$$x_i(t+\varepsilon)\approx x_i(t)+\varepsilon\cdot\frac{dx_i(t)}{dt}=x_i(t)+\varepsilon\cdot\frac{\partial K(\mathbf{p}(t))}{\partial p_i} \\ =x_i(t)+\varepsilon\cdot\frac{\partial\left(\mathbf{p}(t)^T\mathbf{p}(t)/2m\right)}{\partial p_i} = x_i(t)+\varepsilon\cdot\frac{p_i(t)}{m}$$

只要 $\varepsilon$ 夠小的話, 就會夠接近.
同理 $p_i(t+\varepsilon)$ 也能用 (7) 估計出來. 總結為以下 update 方法 (令 $m=1$), 而這個方法稱為 Euler’s method:

$$\begin{align} x_i(t+\varepsilon) = x_i(t)+\varepsilon\cdot p_i(t) \\ p_i(t+\varepsilon) = p_i(t)-\varepsilon\cdot\frac{\partial U(\mathbf{x}(t))}{\partial x_i} \end{align}$$

但致命的缺點是一旦時間長了, 估計就愈來愈不準了. 因此實作上會採用 Leapfrog method: pdf 介紹.
我們先看看兩種方法的精確度差異 (取自 DeepBayes 2019 Summer School Day 5, MCMC slides):

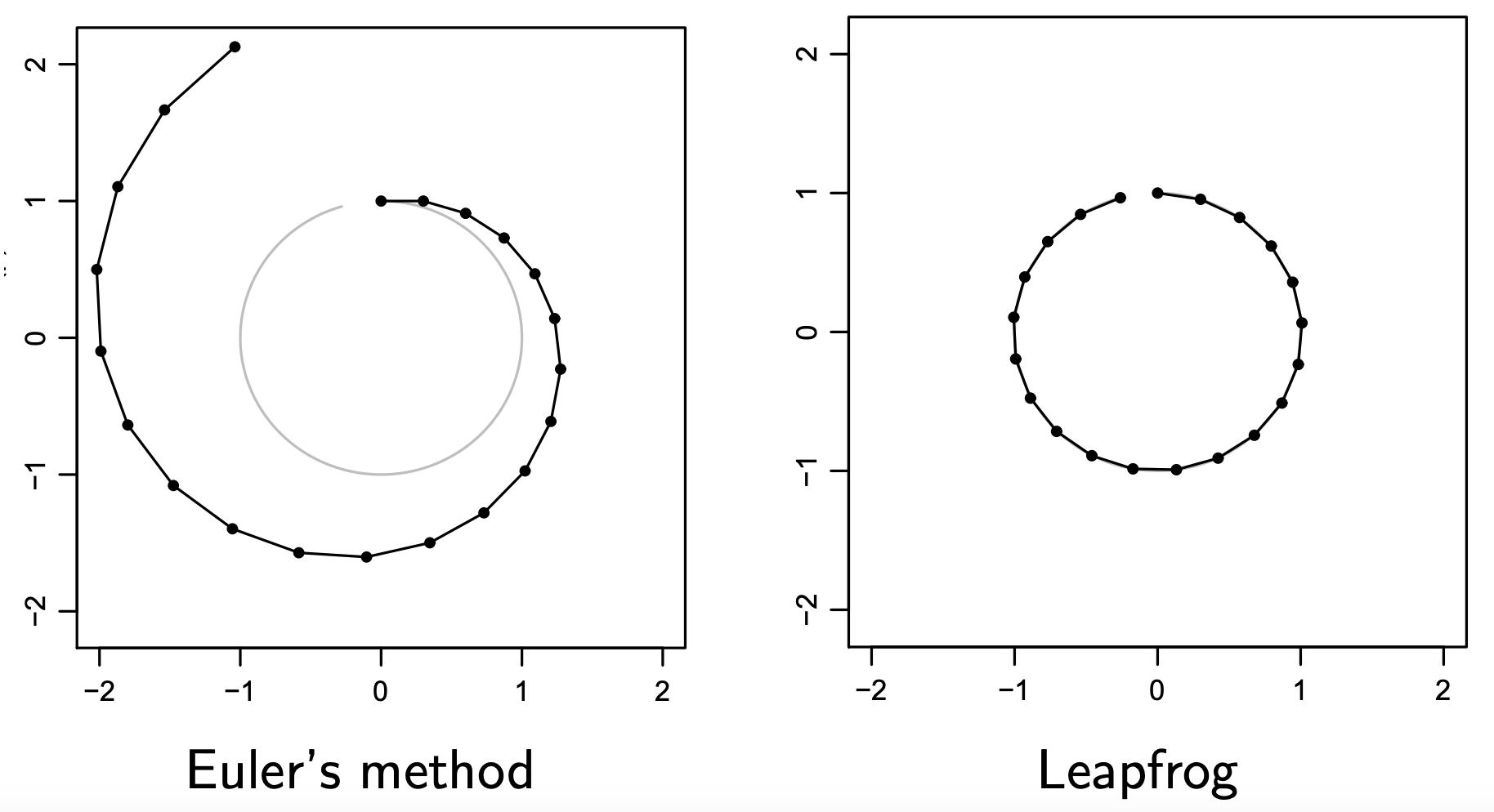
Leapfrog method 描述如下:

$$\begin{align} p_i(t+\varepsilon/2)=p_i(t)-(\varepsilon/2)\cdot\frac{\partial U(\mathbf{x}(t))}{\partial x_i} \\ x_i(t+\varepsilon)=x_i(t)+\varepsilon \cdot p_i(t+\varepsilon/2) \\ p_i(t+\varepsilon)=p_i(t+\varepsilon/2)-(\varepsilon/2)\cdot\frac{\partial U(\mathbf{x}(t+\varepsilon))}{\partial x_i} \end{align}$$

主要的想法是, 在 update $x_i(t+\varepsilon)$ 時 (式 (8)), 原來使用 $p_i(t)$ 來更新, 改成使用”更準的” $p_i(t+\varepsilon/2)$ 來更新, 如同式 (11). 然後 $p_i(t+\varepsilon)$ 分成兩次的 $\varepsilon/2$ steps 來更新.

抱歉沒有嚴謹的數學來證明 error 的 order.

注意到, 我們只需要 $\nabla_\mathbf{x}U(\mathbf{x})$ 就能更新 $(\mathbf{x},\mathbf{p})$!
也就是說只要有 potential energy 的 gradient 就可以模擬 Hamiltonian dynamic!
這點很重要, 因為變成 sampling 方法後等同於這句話: 只要有 score function 就能採樣! 而 score function 怎麼估計, Score Matching 是個好方法.
Sample codes from (Markov Chain Monte-Carlo Solution.ipynb):

def _leapfrog(self, x, v):
    self.energy = []
    for _ in range(self.n_steps):
        v -= 0.5 * self.eps * self.dist.grad_log_density(x)
        x = x + self.eps * v
        v -= 0.5 * self.eps * self.dist.grad_log_density(x)
        self.energy.append(self._energy(x, v))
    return x, v

彈簧例子

參考自 MCMC: Hamiltonian Monte Carlo (a.k.a. Hybrid Monte Carlo)
不知道怎麼來的也沒關係, 反正此時的系統能量為:

$$U(x)=\frac{x^2}{2} \\ K(p)=\frac{p^2}{2} \\ H(x,p)=U(x)+K(p)$$

位置 $x$ 的參考原點定義在彈簧中心, 也就是剛好 potential energy 為 $0$ 的時候. 使用 Leapfrog method 來模擬 Hamiltonian equations 更新狀態 $(\mathbf{x},\mathbf{p})$:

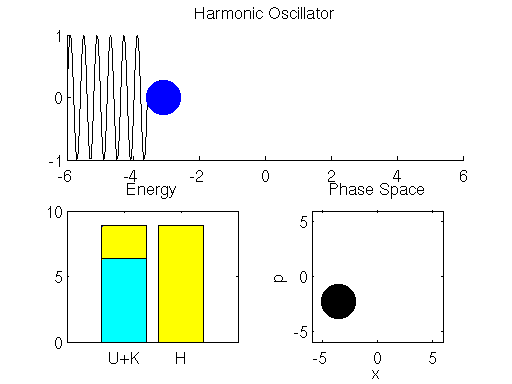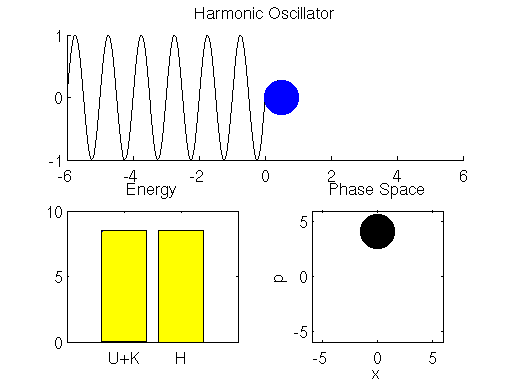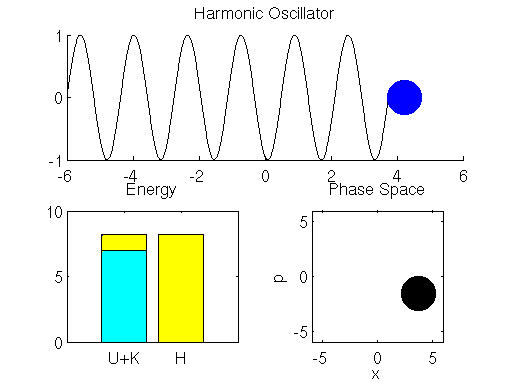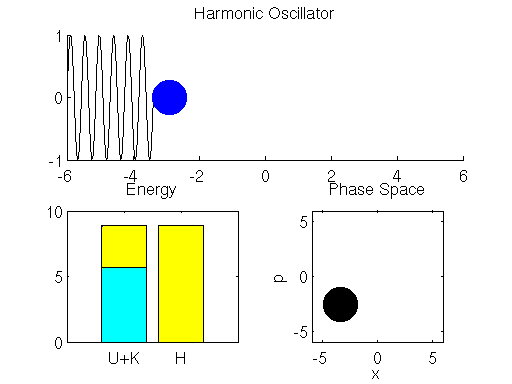
可以看到 Hamiltonian dynamic 的過程, 能量上 (左下角的圖) 只是 potential 和 kinetic energy 的互相交換 (黃色和青色互相消長), 其總能量是不變的.
哎不對~總能量 $H$ 的那條全黃色的 bar 沒有固定不動啊, 看起來還是會小幅度上上下下的.
是的, 縱使用了 Leapfrog method, 還是會漂移, 這是因為我們對時間離散化造成的. 想要 error 更小, 就必需切更細碎的時間去逼近.
另外需要特別說明, 右下角的 “Phase Space” 圖, 畫出了 $(x,p)$ 狀態值的移動路徑. 由於能量守恆, 這路徑代表了相同的 Hamiltonian energy. 為什麼要特別說明這點, 在後面講 sampling 的時候會再次提到.

能量怎麼看成機率分佈? 或反過來?

給定能量 $E(x)$, 總是可以用下式變成機率分佈 (Gibbs distribution):

$$p(x)=\frac{1}{Z}e^{-E(x)}$$

$Z$ 就是一個 normalization constant 變成機率分佈用的. 所以能量愈大表示的機率密度就愈小.
我們來將 Hamiltonian energy 變機率分佈看看:

$$p(\mathbf{x},\mathbf{p})=\frac{1}{Z}e^{-H(\mathbf{x},\mathbf{p})} \\ \propto e^{-(U(\mathbf{x})+K(\mathbf{p}))} =e^{-U(\mathbf{x})}e^{-K(\mathbf{p})} =p(\mathbf{x})p(\mathbf{p})$$

這裡可以發現 $\mathbf{x}$ 與 $\mathbf{p}$ 互相獨立.
原本從物理那邊我們是先定義了能量, 再利用 Gibbs distribution 變成了機率分佈.
現在我們反過來操作: 先定義我們要的機率分佈, 然後反推能量長什麼樣.

🤔 題外話, 寫到這我就在想, 反過來從先定義機率分布再推導能量是不是仍然能滿足 energy conservation?
i.e. 能量隨時間不變.
$$\begin{align} \frac{dH(x,p)}{dt}=0 \end{align}$$
但其實不用擔心, 因為只要用 Hamiltonian equations (6), (7) 去更新狀態, 就會滿足 energy conservation.
我們考慮 1-D case 即可, 能量為 $H(x(t),p(t))$, 滿足 (6) and (7) 並觀察
$$\frac{dH(x(t),p(t))}{dt}=\frac{dH}{dx}\frac{dx}{dt}+\frac{dH}{dp}\frac{dp}{dt} \\ \text{by }(6)=\frac{dH}{dx}\frac{dH}{dp}+\frac{dH}{dp}\frac{dp}{dt} \\ \text{by }(7)=\frac{dH}{dx}\frac{dH}{dp}-\frac{dH}{dp}\frac{dH}{dx}=0$$

因為互相獨立, 我們可以先定義 $\mathbf{p}$ 是 normal distribution $\mathcal{N}(\mathbf{p}|0,I)$

$$p(\mathbf{p})=\frac{1}{Z_\mathbf{p}}e^{-\frac{\mathbf{p}^T\mathbf{p}}{2}}$$

可以看得出來其 (kinetic) energy 為:

$$\begin{align} K(\mathbf{p})=\frac{\mathbf{p}^T\mathbf{p}}{2} \end{align}$$

然後不要忘記我們的目的是要從一個目標分佈 $p^*(\mathbf{x})$ 取樣, 因此 $\mathbf{x}$ 的機率分佈就直接定義成目標分佈. 而其 (potential) energy 為:

$$\begin{align} p^*(\mathbf{x})=\frac{1}{Z_\mathbf{x}}e^{-U(\mathbf{x})} \\ \Longrightarrow U(\mathbf{x})=-\log p^*(\mathbf{x}) + \text{const.} \end{align}$$

還記得我們之前說過這句話嗎? “我們只需要 $\nabla_\mathbf{x}U(\mathbf{x})$ 就能更新 $(\mathbf{x},\mathbf{p})$!”
因此 (16) 的 $\text{const.}$ 就不重要了, 所以 potential energy 這麼定義就可以了:

$$\begin{align} U(\mathbf{x})=-\log p^*(\mathbf{x}) \end{align}$$

MHC 採樣過程

好了, 到目前為止我們藉由設定好的 distribution $p^*(\mathbf{x}),\mathcal{N}(\mathbf{p}|0,I)$, 可以找到對應的 energy functions $U(\mathbf{x}),K(\mathbf{p})$.
那就可以套用 Hamiltonian equations (6), (7) 來模擬能量不變的情形下, $(\mathbf{x},\mathbf{p})$ 隨時間的變化.
給定一個初始狀態 $(\mathbf{x}_0,\mathbf{p}_0)$ 可以得到:

$$(\mathbf{x}_0,\mathbf{p}_0)\xrightarrow[]{(6)(7)}(\mathbf{x}_1,\mathbf{p}_1)\xrightarrow[]{(6)(7)}(\mathbf{x}_2,\mathbf{p}_2)\xrightarrow[]{(6)(7)}...$$

其中 $H(\mathbf{x}_0,\mathbf{p}_0)=H(\mathbf{x}_1,\mathbf{p}_1)=...$
實作上由於每一次 (6), (7) 的更新都採用很小的 $\varepsilon$ (Leapfrog sample codes 裡的 self.eps), 這樣才能確保夠準確.
但我們也希望能夠走遠一些 (這對 multi-modual 的 distribution 很有幫助, 如下圖所示), 所以會跑個 $T$ 步 updates (Leapfrog sample codes 裡的 self.n_steps)

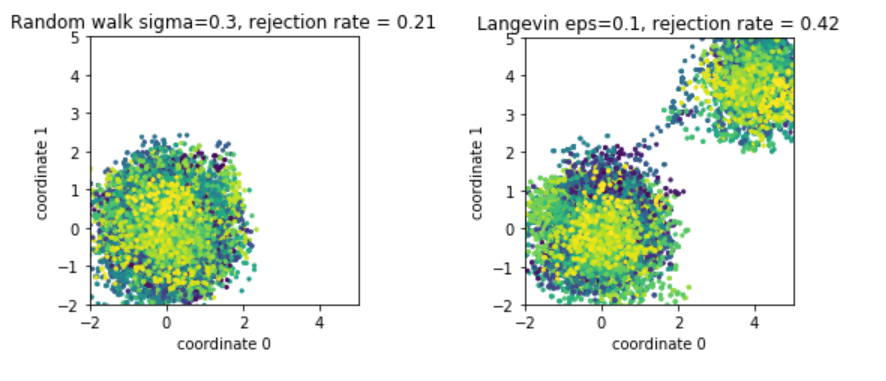
但就算如此, 由於 energy conservation (13) 的關係, $\mathbf{x}$ 只會在 phase space 上具有相同能量的 contour 上採樣.
(Phase space 定義為 $(\mathbf{x},\mathbf{p})$ 的空間)
為了能夠採樣出其它的點, 我們需要換到其他能量的 contour, 因此改變 $\mathbf{p}$, 即對它重新採樣即可.
(follow 之前定義好的分佈 $\mathcal{N}(\mathbf{p}|0,I)$).
但是別忘了, Hamiltonian MC 所提出的採樣是 Metorpolis-Hastings 的 proposal distribution. 所以也需要有 accept/reject, 但也得益於 energy conservation 所以會有非常高的 accept rate. 因而採樣效率很好.
總結一下 HMC 方法 [ref 3]:

而 Tuning HMC 有幾個要點 [ref 3]:

一般來說要控制 rejection rate 在 $[1/4,3/4]$ 之間會比較好. 還有多跑幾個 threads 來確認收斂狀況.

References

马尔可夫链蒙特卡洛算法 (二) HMC
MCMC: Hamiltonian Monte Carlo (a.k.a. Hybrid Monte Carlo)
DeepBayes 2019 Summer School Day 5, MCMC slides
MHC sample codes from (https://github.com/bayesgroup/deepbayes-2019/blob/master/seminars/day5/Markov Chain Monte-Carlo Solution.ipynb)
Leapfrog method: https://www2.atmos.umd.edu/~ekalnay/syllabi/AOSC614/NWP-CH03-2-2.pdf