Introduction of Probably Approximately Correct (PAC) 林軒田課程筆記

這是林軒田教授在 Coursera 機器學習基石上 (Machine Learning Foundations)—Mathematical Foundations Week4 的課程筆記.
說明了為什麼我們用 training data 學出來的 model 可以對沒看過的 data 有泛化能力, 因此機器學習才有可能真正應用上.
課程單元的這句話總結得很好 “learning can be probably approximately correct when given enough statistical data and finite number of hypotheses”
以下為筆記內容

怎麼說都你對, training data 外的 predition

$\mathcal{D}$ is training data, learning algorithm 找到的 function $g$ 對 $\mathcal{D}$ 完美的 predict, 但 training data 外的資料也能保證很好嗎?

所以對 training data $\mathcal{D}$ 找 hypothesis 沒問題嗎??
由 Probably Approximately Correct (PAC) 出發, 告訴我們當 data 量夠大的時候是沒問題的.

大概差不多正確 Probably Approximately Correct (PAC)

Hoeffding’s Inequality

請看投影片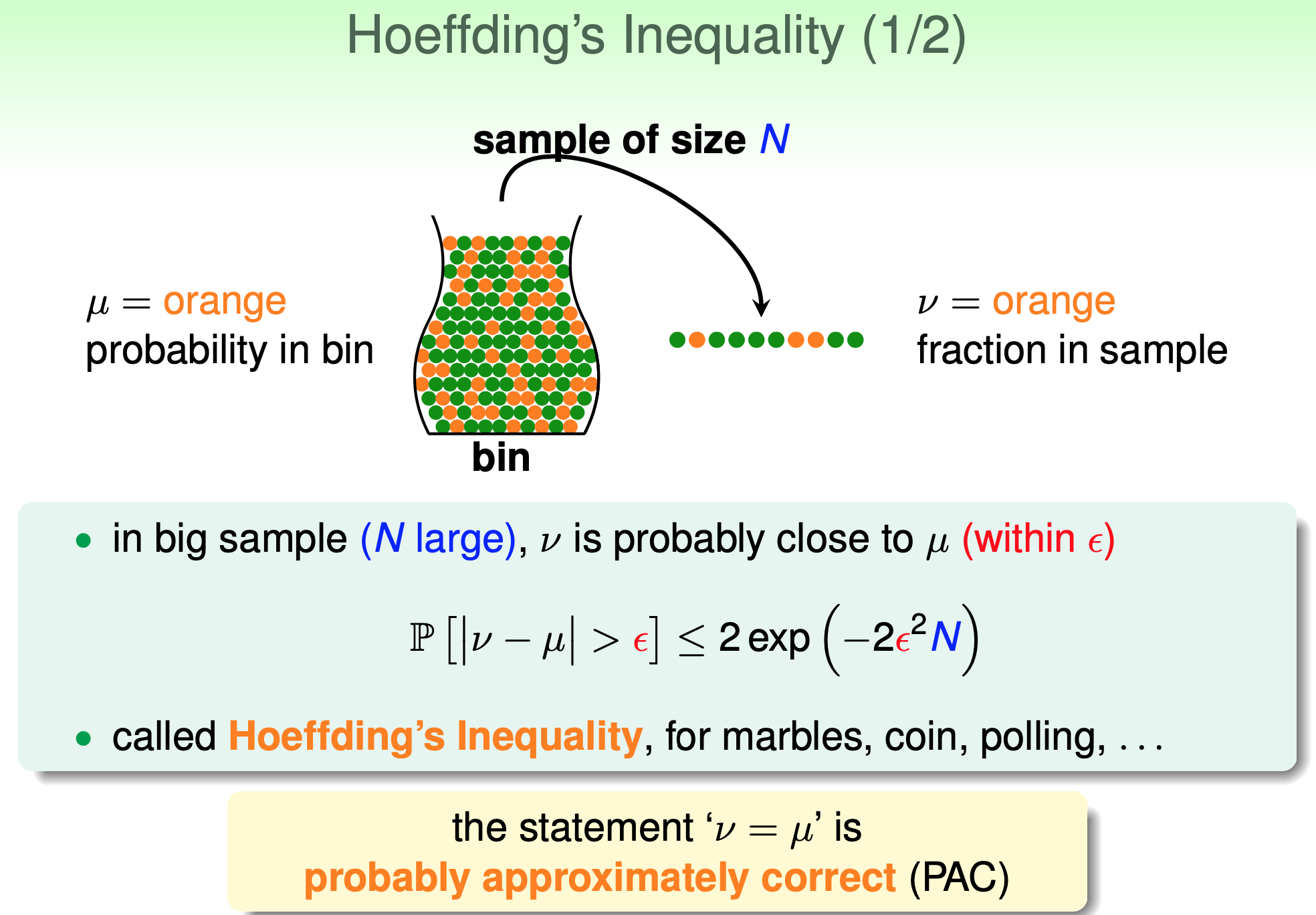
$\mathbb{P}[|\nu-\mu|>\epsilon]$ 想成壞事發生的機率. 所以告訴我們, 壞事發生的機率有個 upper bound. 就是當 $N$ 夠大, 壞事發生的機率就很小.
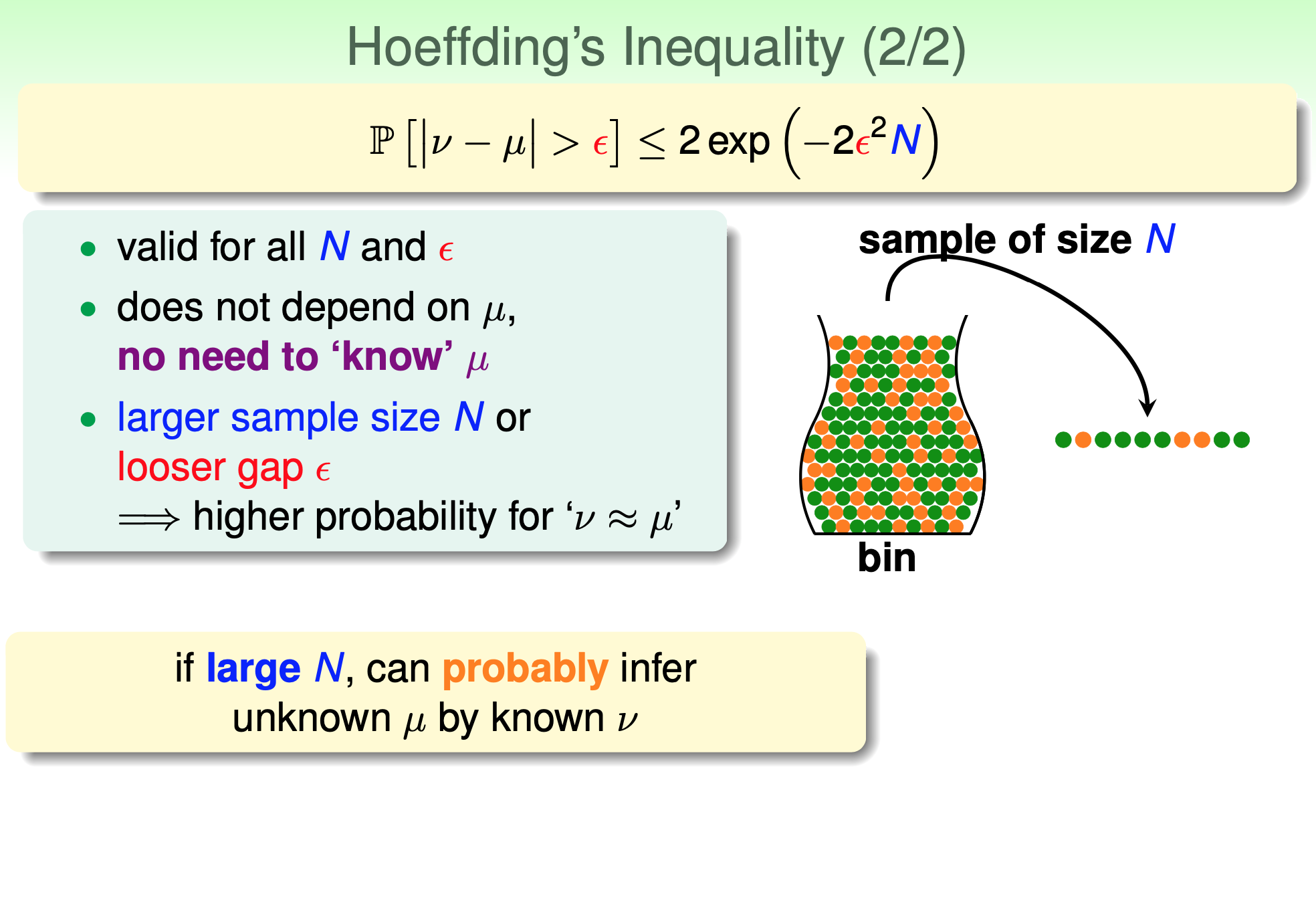Wiki: Hoeffding’s inequality
Let $X_1,…,X_N$ be independent r.v.s such that $a_i\leq X_i\leq b_i$ almost surely. Consider $S_N=X_1+…+X_N$. Then for all $t>0$,
$$\begin{align} P(S_N-\mathbb{E}[S_N]\geq t)\leq \exp\left( -\frac{2t^2}{\sum_{i=1}^N(b_i-a_i)^2}\right) \\ P(|S_N-\mathbb{E}[S_N]|\geq t)\leq 2\exp\left( -\frac{2t^2}{\sum_{i=1}^N(b_i-a_i)^2}\right) \end{align}$$ 以老師的投影片來說, random variable $X_i$ 表示是不是橘球, 是的話就是 $1$, 不是就是 $0$. 所以 $0\leq X_i \leq 1$.
因此 $S_N=X_1+…+X_N$ 就表示 $N$ 個球中是橘球的數量的 random variable. 然後帶入 wiki 的公式就可以跟老師的投影片結果對照起來. 注意 wiki 使用 $S_N$, 但投影片用的是 $\nu=S_N/N, \mu=\mathbb{E}[S_N]/N$. 所以 $t=N\epsilon$.

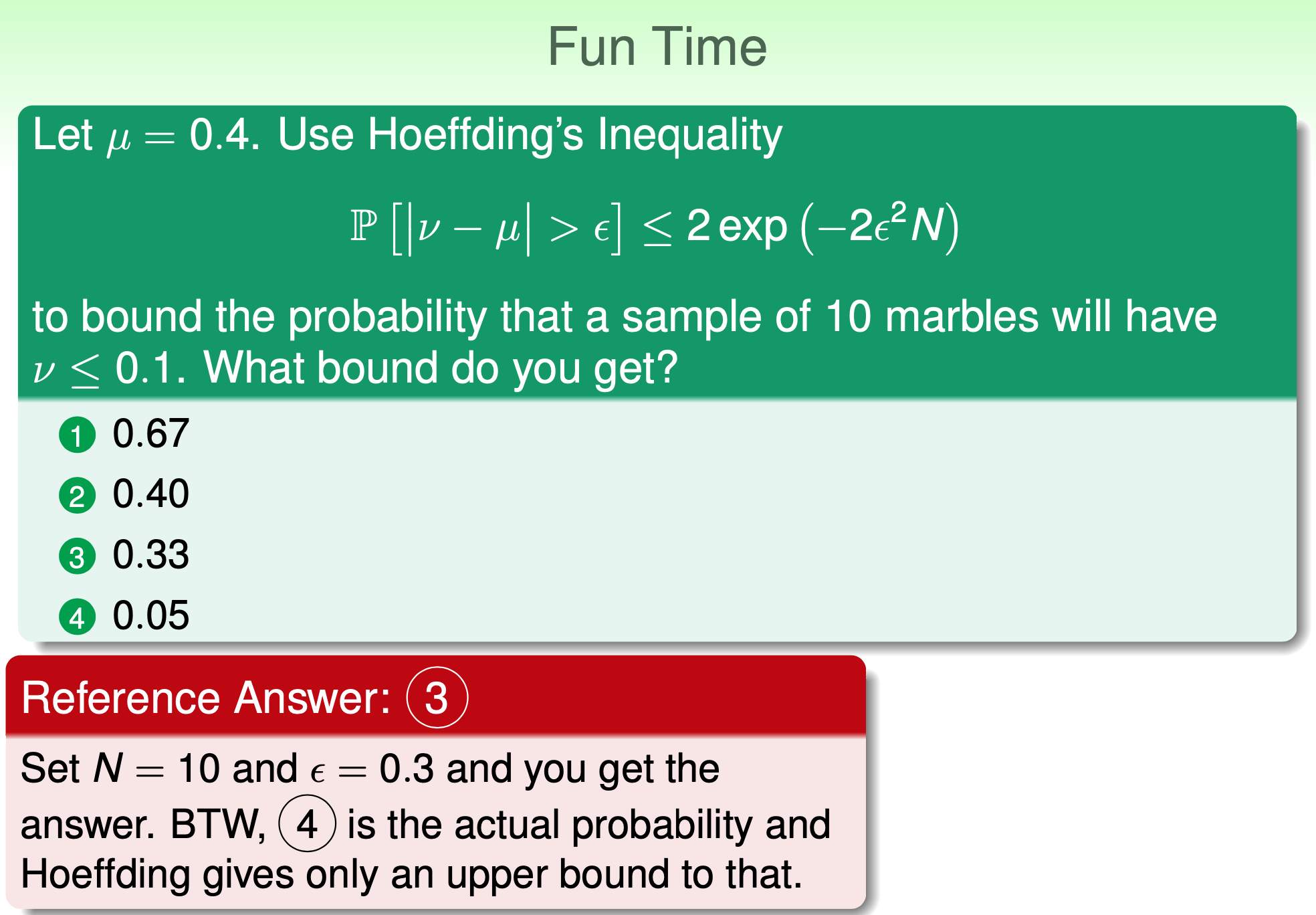所以對 training data $\mathcal{D}$ 不過 Hoeffding’s inequality 它的 bound 不是很 tight.

Connection to Learning

上面罐子抽彈珠的例子, 其實跟 ML 要怎麼確認找到的 $h$ 是不是跟 oracle $f$ 夠像是同一個問題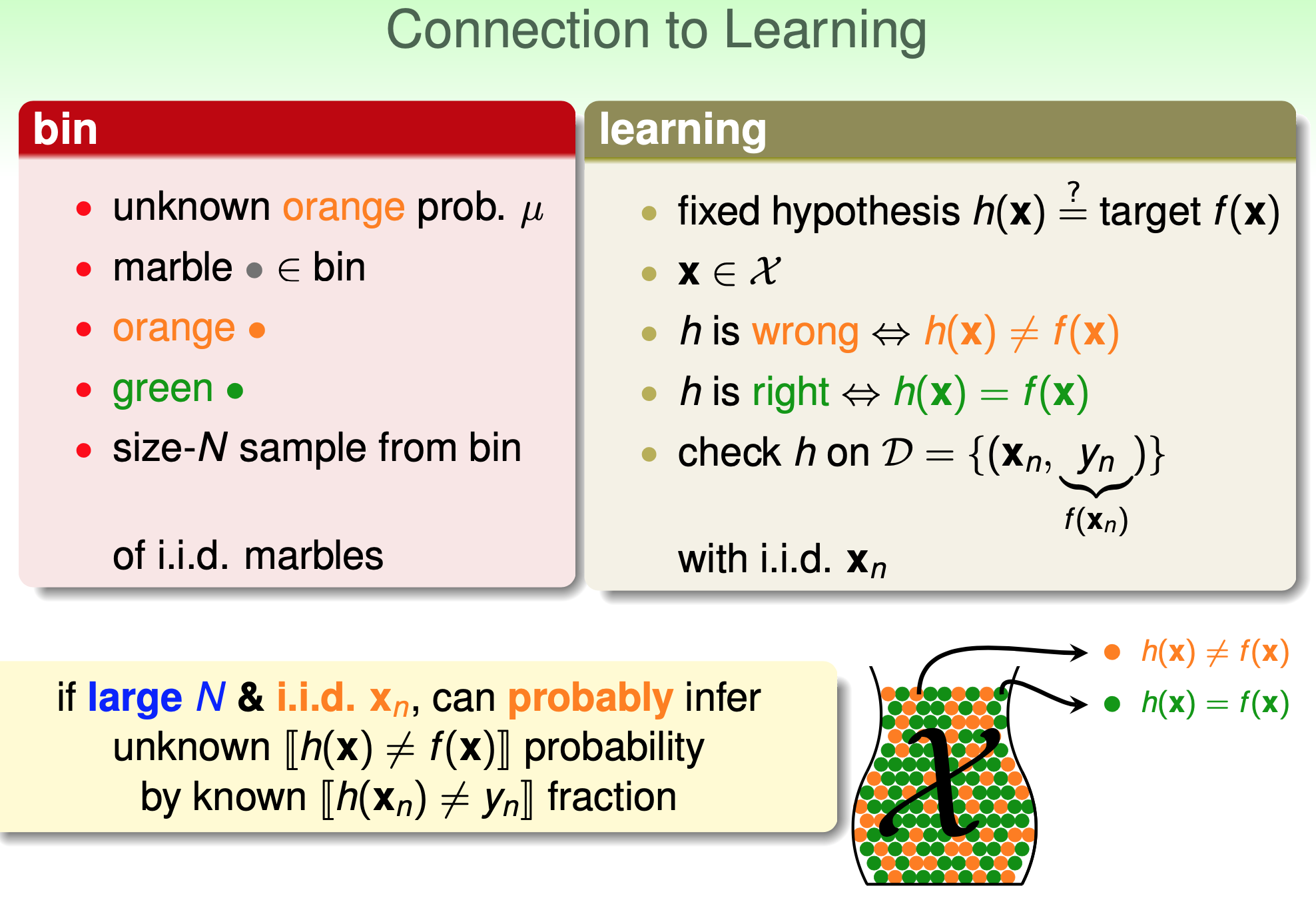
把整個 $\mathcal{X}$ 當成是整個罐子的彈珠, 而 training dataset $\mathcal{D}$ 是抽樣出來的 $N$-sample.
對某一個 $x\in\mathcal{X}$, $h(x)\neq f(x)$ 就是橘色彈珠, 否則就是綠色彈珠. 則 $\mu$ 就是 $\mathbb{E}_{out}$, $\nu$ 就是 $\mathbb{E}_{in}$.
所以原來壞事發生的機率 $\mathbb{P}[|\nu-\mu|>\epsilon]$ 在這裡變成 $\mathbb{P}[|\mathbb{E}_{in}-\mathbb{E}_{out}|>\epsilon]$ (inside-test 和 outside-test 的錯誤率差太多的機率)
則根據 Hoeffding’s Inequality, 對某一固定的 hypothesis $h$ 在 training data 上的表現和 out-of-sample 的 data 表現大概接近.
$$\mathbb{P}\left[|E_{in}(h)-E_{out}(h)|>\epsilon\right]\leq 2\exp\left(-2\epsilon^2N\right)$$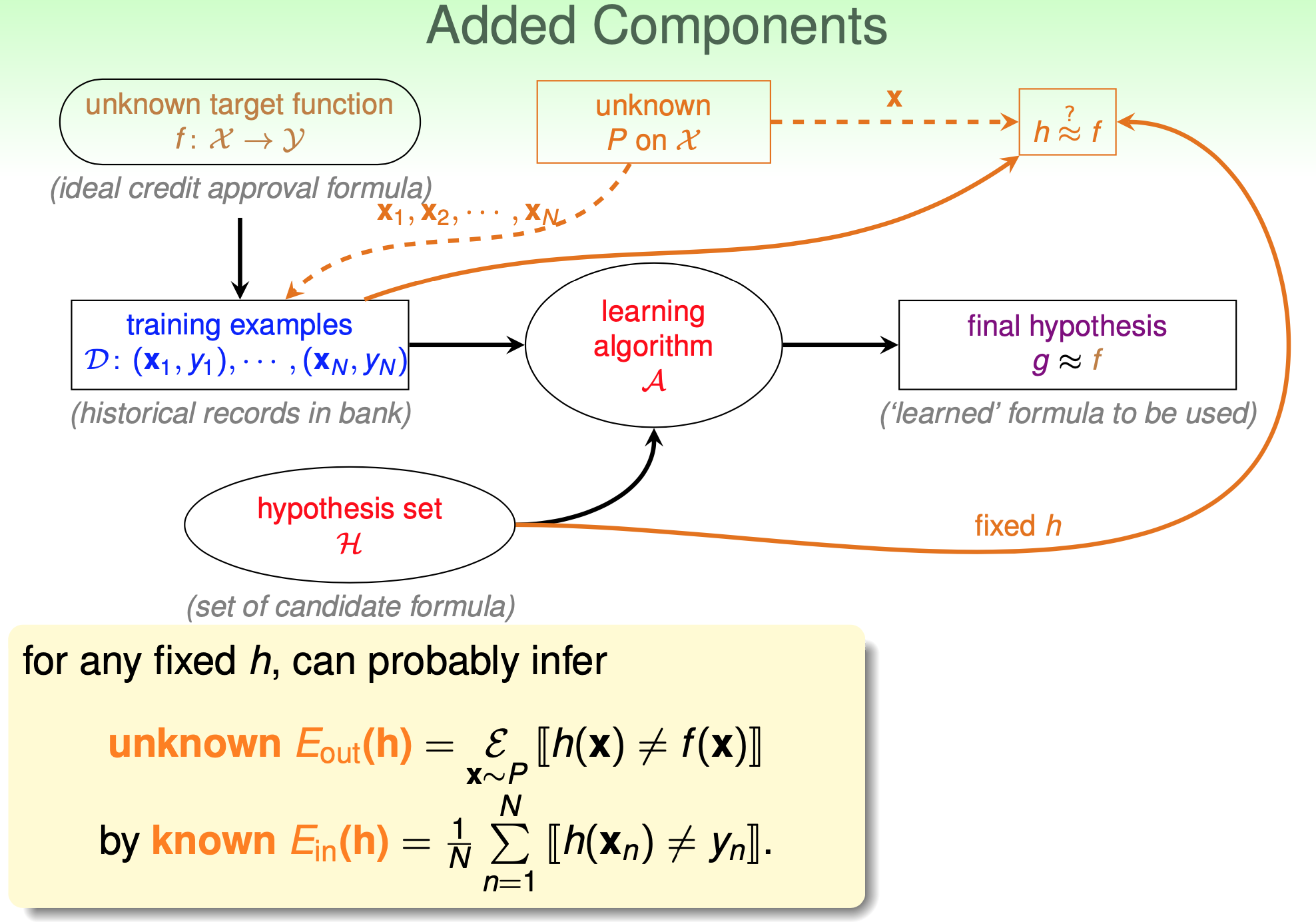
上圖中, 先不看 learning algorithm $\mathcal{A}$ 以及它挑出來的 final hypothesis $g$ 那兩塊.
注意到, 目前所說的是指已經固定一個 $h$ 了, 然後我們可以用 unknown probability $P$ 採樣出來的 set $\mathcal{X}$ 得到 $\mathbb{E}_{in}\approx\mathbb{E}_{out}$. 意思就是這個 $h$ 不能針對 $\mathbb{E}_{in}$ 去學習找出來.
再白話一點 “固定一個 $h$” 意思是罐子裡彈珠的顏色已經先固定了! Hoeffding’s 只是告訴我們抽樣的資料 (size $N$ 的彈珠, set $\mathcal{D}$) 查看到的錯誤率跟整個罐子的錯誤率會很接近. 所以當然不能針對抽出來的資料再來挑選 $h$, 這樣等於事後改變彈珠顏色.
也就是說這時候的 $\mathbb{E}_{in}(g)$ 指的是用 verification data 來看 error, 或許叫 $\mathbb{E}_{ver}$ 比較好. 而真正的 training data 給 learning algorithm $\mathcal{A}$ 用來挑 $g$.
這就是 Verification dataset 在做的事情.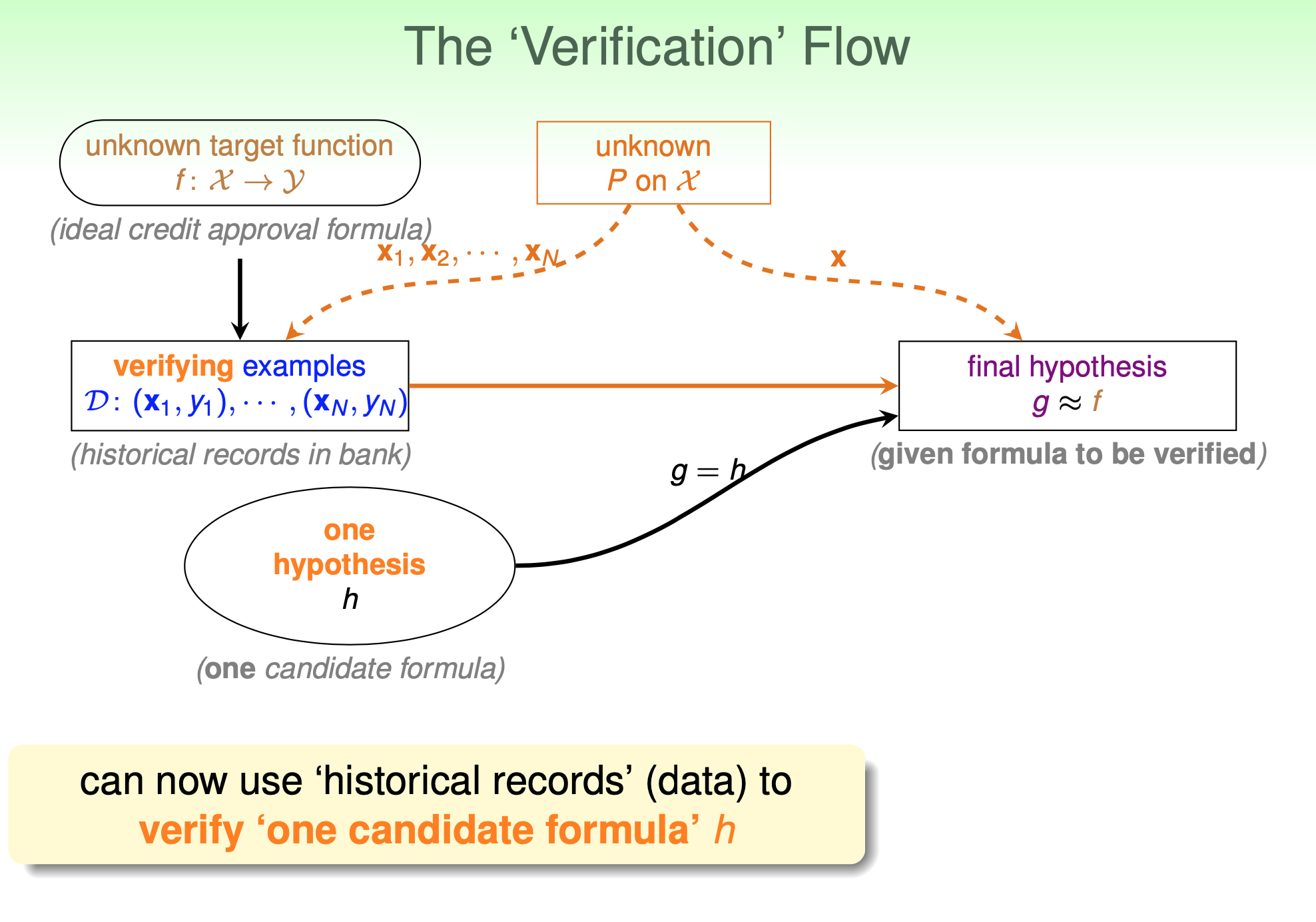

💡 下一段所講的 $\mathbb{E}_{in}$ 其實指的是 $\mathbb{E}_{ver}$, training data $\mathcal{D}$ 其實是 verification data

Connection to Real Learning

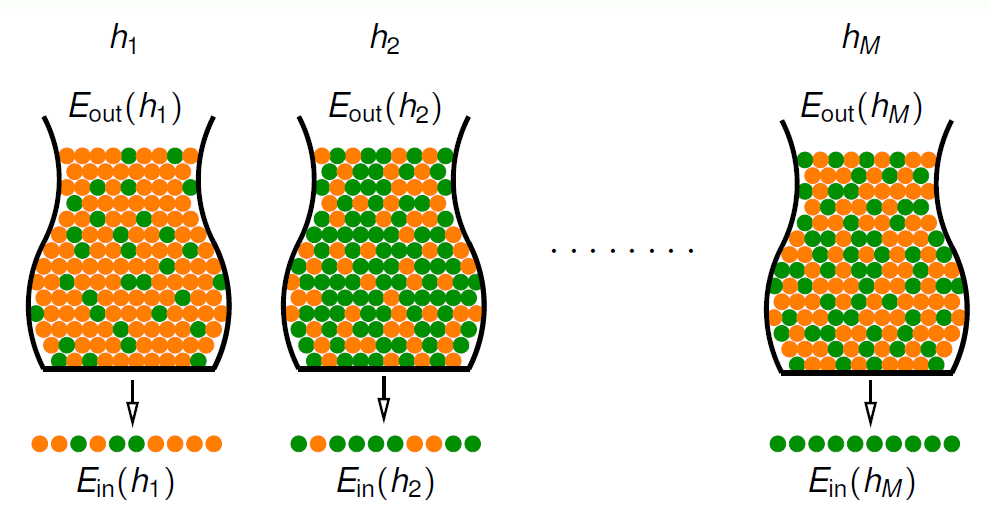
一個固定的 hypothesis $h$ 會對應到一種彈珠顏色分布情形, 橘色代表它跟 oracle $f$ 不一樣的 input $x$.
Hoeffding 告訴我們, 對這一個 $h$ 我們看 $\mathbb{E}_{in}(h)$ 大概差不多等於 $\mathbb{E}_{out}(h)$. 換句話說 BAD 的機率很小, 所以我們可以相信 $\mathbb{E}_{in}(h)$ 的評估結果.

$$\mathbb{P}_{\mathcal{D}}[{\color{orange}{\text{BAD }}} \mathcal{D}] = \sum_{D\in\mathcal{D}}{\mathbb{P}(D)\cdot 1[D \text{ is}{\color{orange}{\text{ BAD}}}]}$$ Hypothesis set $\mathcal{H}$ 通常會有無窮多個 hypothesis, 我們先假設它只有 $M$ 個就好.

無窮多的 case 之後課程會介紹.

結果對 sampling 出來的 data (training data), 我們發現其中有一個 hypothesis 表現全對, 我們可以選它嗎? 當然不能. 那不能的話, learning algorithm $\mathcal{A}$ 根據 training data (這裡其實指的是 verification data) 挑最好的 $\mathbb{E}_{in}$ 不就沒意義了?

別緊張, 我們先看一下所有 hypothesis 對應 training data 的表: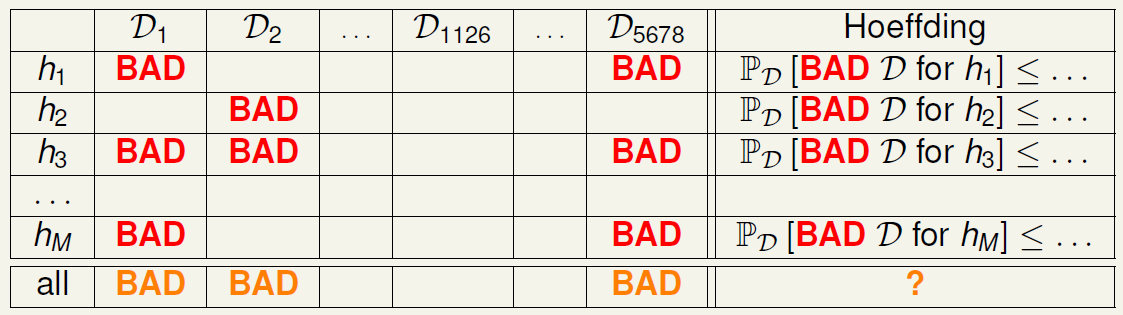
關鍵在 column, 因為 learning algorithm $\mathcal{A}$, 對某一 sampling 出來的 training data $\mathcal{D}_i$ (這裡其實指的是 verification data) 會挑一個 error 最小的 hypothesis. 但會挑到哪一個不知道 (因為 $\mathcal{A}$ 是用真正的 training data 挑的, 不是用 $\mathcal{D}_i$ 挑的, 別忘了 $\mathcal{D}_i$ 是 verification data), 所以任何的 $h_i$ 都有可能被 $\mathcal{A}$ 挑到.
所以只要 column 中有某一個 hypothesis 是 BAD 的話, learning algorithm 就失去作用了. 對於 all 最後那個 row 來說, 只要有一個 hypothesis 是 BAD, all 就算 BAD. 如同 PAC 一樣, 我們希望最後一個 row BAD 的機率越低愈好.
評估一下這樣情況下, 發生 BAD 的機率: