Score Matching 系列 (五) SM 加上 Langevin Dynamics 變成生成模型

發表於 | 分類於 | [object Object]

主要內容為這篇文章 “Generative Modeling by Estimating Gradients of the Data Distribution“

背景知識

Score-based generative modeling 的兩個核心概念:

  1. Score matching (SM):
    使用 score matching loss 讓 NN 直接學 score function: $\nabla_x\log p_{data}(x)$, 其中 $p_{data}(x)$ 為 data p.d.f.
    因此我們有一個 NN: $s_\theta(x)\approx \nabla_x\log p_{data}(x)$
    Score matching 在做什麼, 請參考系列文章:

  2. Langevin dynamics:
    Langevin dynamics 可以使用 score function, i.e. $\nabla_x\log p_{data}(x)$, 來取 sample, 取出來的 sample 具有 $p_{data}(x)$ 的分佈
    而我們已經用一個 NN $s_\theta(x)$ 來逼近 score function 了, 因此可以用 $s_\theta(x)$ 來取 sample, 步驟如下:
    給定一個固定的 step size $\epsilon>0$, initial value $z=\tilde{x}_0\sim\pi(x)$, 其中 $\pi(x)$ 是固定的 prior distribution, and $z_t\sim\mathcal{N}(0,I)$

    $$\tilde{x}_t = \tilde{x}_{t-1}+\frac{\epsilon}{2}\nabla_x\log p_{data}(\tilde{x}_{t-1})+\sqrt{\epsilon}z_t \\ \approx \tilde{x}_{t-1}+\frac{\epsilon}{2}s_\theta(\tilde{x}_{t-1})+\sqrt{\epsilon}z_t$$ 當 $\epsilon\rightarrow 0$, $T\rightarrow\infty$ 則 $\tilde{x}_T$ 等同於從 $p_{data}(x)$ 取樣!
    我們在這篇文章 忘記物理也要搞懂的 Hamiltonian Monte Carlo (HMC) 筆記
    非常仔細得解釋了為什麼可以這麼做, 注意到其實這裡涉及了很多知識, 依序包含 MCMC, Metropolis Hastings, Hamiltonian Dynamic, 最後才關聯到 Langevin Dynamics. 不過只想單純使用的話, 上面的描述就足夠.

藉由 Score Matching + Langevin Dynamics (SMLD), 我們發現如果成功學到 score function, 則可以從 random noise $z$ 產生符合 data distribution 的 sample.
而這正是 generative model 在做的事情, 此種方法論文稱為 SMLD
但是直接訓練出來的 SMLD 在真實資料上會有兩個問題導致做不好, 接著論文裡說明是什麼原因以及解決方法

兩個主要問題

  1. The manifold hypothesis:
    Score matching (SM) 要做得好是基於資料分布是布滿整個 space 的 (意思是 data pdf 的 rank 沒有降低), 然而真實資料都是在低維度的 manifold. 這會讓 SM 做不好 (even using Sliced SM). 例如3維空間中, 資料分佈的 manifold 只有 rank 2 (平面), 或是只剩下 rank 1 (線)
  2. Low data density regions:
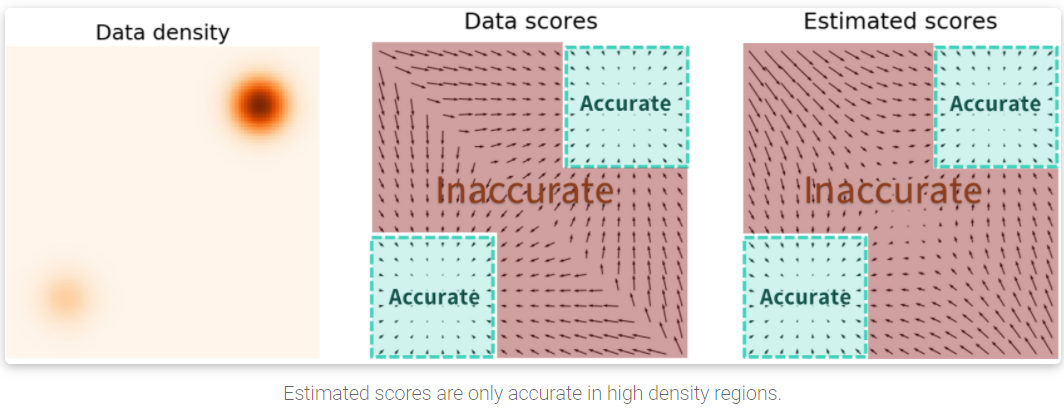
    在 density 密度低的地方, 由於 training data 也很少, 導致這些地方 SM 根本估不準. (見下圖)
    另一方面, 這個問題也會影響 Langevin dynamics 的採樣:
    舉例來說, 如果資料分布是由兩個 disjoint 的 mode density 構成 (e.g. GMM with 2 mixtures), 則一開始的 initial 在哪個資料分布就完全決定了會收斂在哪邊. 這種現象稱為 multi-modal 的 mixing problem. 同時不好的 score 估計也會導致 Langevin dynamics 無法有效跑到對的方向, 因而收斂很慢

解決辦法

要解決第一個問題 (manifold hypothesis) 可以透過加入 Gaussian noise 緩解, 因為會使得分布充滿整個空間, 不再只存在低維度的 mainfold.

上圖左是使用了 SSM 但沒加噪, 可以看到訓練不起來. 上圖右則加了非常小的噪聲 (人眼無法分辨), loss 就能穩定下降!
既然加了一點 noise 就可以 train 起來了, 那就用此學出來的 “接近真實 clean 的 noisy 分布” 去用 Langevin dynamics 採樣看看
結果發現還是沒法採樣出有效的影像:

上圖 (a), (b) and (c) 的每一個 row 左到右表示 Langevin dynamics 的演化過程. 發現採樣不出有效 samples. 不同 rows 表示不同的 random noise $z$ 的結果.
我們學到了接近 clean 的 score function 分佈了, 為何無法用 Langevin dynamics 採樣出來呢?
原因是上面說的第二個問題: multi-modal 的 mixing problem. 而要解決, 可以將加入的 Gaussian noise level 加大 (更廣), 這樣可以讓低密度的地方變少, 因此 scores 就都準了.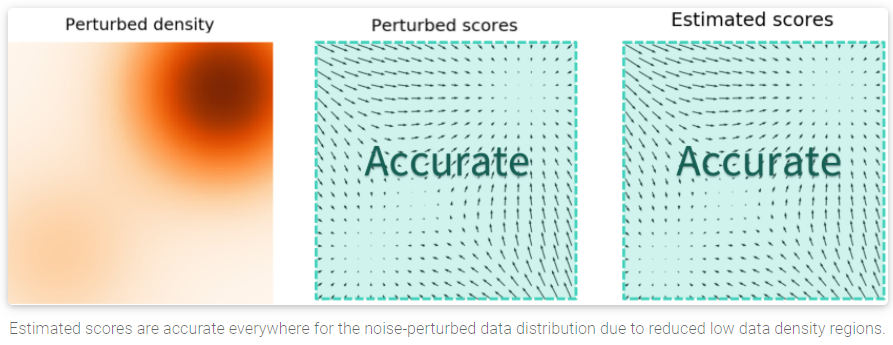

但也只能學到 noisy 的分布 (跟 DSM 缺點一樣)!
因此, 論文的作法就是學一個 Noise Conditional Score Networks (NCSN): 也就是原來的不同 noise level 都會訓練出對應的 score networks, 現在直接用一個 nework 吃 noise level 當 condition 來訓練就好. 藉由這樣的做法, 可以將 noise 從很大漸漸變小, 從而還原到真實的資料分布
也因為我們有不同 noise 程度的 data 分布 (NCSN approximates 的分佈), 原來的 Langevin dynamics 需要改成 annealed 版本, 這樣也能解決 multi-modal problem.

因為最開始的 noisy 分布是 noise 最大的情況, 此時不同 modes 之間區別不大, 且 low density 區域也很少

Annealed Langevin dynamics 算法如下:

$\{\sigma_i\}_{i=1}^L$ 是一個正的等比數列, 表示每不同的 noise level 程度, 我們讓 $\sigma_1$表示最大噪聲等級, $\sigma_L$ 為最小噪聲等級且接近 $0$, 表示滿足:

$$\frac{\sigma_1}{\sigma_2}=\dots=\frac{\sigma_{L-1}}{\sigma_L}>1$$

核心概念就是用 Langevin dynamics 從 $q_{\sigma_{i-1}}(x)$ (較大噪聲的估計分佈) 採樣, 然後該 sample 當成初始 sample 再從 $q_{\sigma_i}(x)$ (較小噪聲的估計分佈) 中繼續用 Langevin dynamics 採樣.
藉由從大噪聲一路採樣到小噪聲的分佈, 我們就能接近原始情況下的採樣
step size $\alpha_i$ 會漸漸變小, 如演算法的第3列
這個 step size $\alpha_i$ 的選擇是為了讓 Langevin dynamics 的 “signal-to-noise” ratio:
$$\frac{\alpha_i s_\theta(x,\sigma_i)} {2\sqrt{\alpha_i}z}$$

與加的 noise level $\sigma_i$ 無關 (作者在經驗上發現 $\|s_\theta(x,\sigma)\|_2\propto 1/\sigma$, 代入上面的 SNR ratio 會發現與 $\sigma_i$ 無關)

結果

藉由 NCSN 和 annealed Langevin dynamics 方法, 論文可以很好的產生影像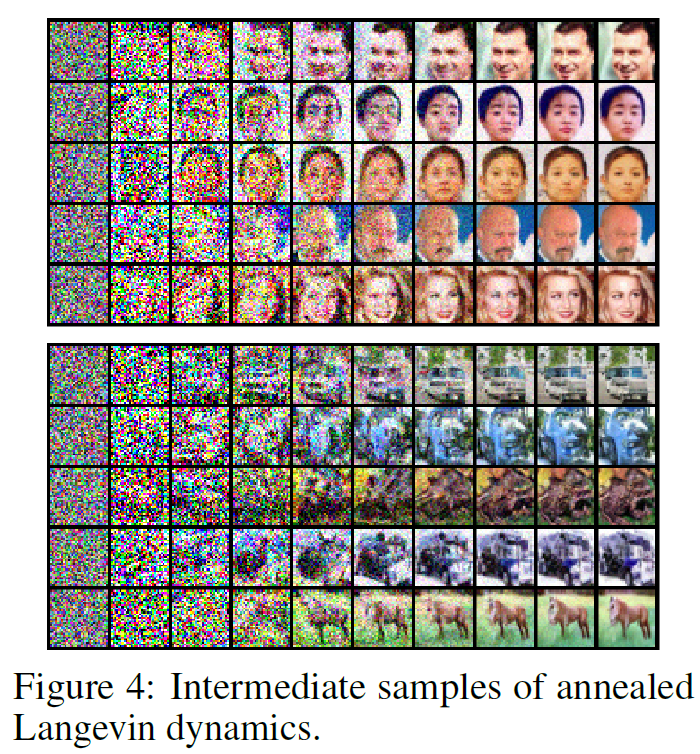

For image Inpainting, sampling 算法如下

沒有被遮擋的地方就是原本的 image + noise $\tilde{z}$, 遮擋的地方是從 annealed Langevin dynamics 產生的
結果如下:

討論

使用 NCSN 的 network 架構學習 score function. 一但有了 score function, 就可以使用 annealed Langevin dynamics 採樣. 因此生成模型就完成了

💡 SMLD = NCSN + annealed Langevin dynamics

但這樣的做法還有一些問題, 雖然 NCSN 使用不同尺度的 noise 訓練, 但 noise 的尺度怎麼選? Langevin dynamics 的 step size 參數 $\epsilon$, 以及次數 $T$ 怎麼定?
這些都必須仔細調整, 才會有比較好的效果. 也因此到這篇文章為止 (2019) 只能產生較小的圖 (32x32 以下)
所以在接下來的一篇文章 “Improved Techniques for Training Score-Based Generative Models”, 2020, Yang Song 從理論上探討了這些建議的設定, 結果能讓 SMLD 的生成模型穩定產生 64x64, 256x256 的結果.
更進一步, Yang Song 在 ICLR 2021 的論文 “Score-Based Generative Modeling through Stochastic Differential Equations” 將 SMLD 與 Diffusion Probabilistic Modeling (DPM) 的生成模型透過 SDE 的 framework 統一起來.
在這架構下, SMLD 與 DPM 其實是一體兩面, 不同的解讀而已! 太讓人讚嘆了! 在該篇結果已經能做到 1024x1024 的高解析度圖片, 這讓人非常期待 score-based generative modeling 接下來的發展!

精彩精彩!