發表於 | 分類於

看完本文會知道什麼是 fake quantization 以及跟 QAT (Quantization Aware Training) 的關聯
同時了解 pytorch 的 torch.ao.quantization.fake_quantize.FakeQuantize 這個 class 做了什麼

Fake quantization 是什麼?

我們知道給定 zero ($z$) and scale ($s$) 情況下, float 數值 $r$ 和 integer 數值 $q$ 的關係如下:

$$\begin{align} r=s(q-z) \\ q=\text{round_to_int}(r/s)+z \end{align}$$ 其中 $s$ 為 scale value 也是 float, 而 $z$ 為 zero point 也是 integer, 例如 int8
Fake quantization 主要概念就是用 256 個 float 點 (e.g. 用 int8) 來表示所有 float values, 因此一個 float value 就使用256點中最近的一點 float 來替換
則原來的 floating training 流程都不用變, 同時也能模擬因為 quantization 造成的精度損失, 這種訓練方式稱做 Quantization Aware Training (QAT) (See Quantization 的那些事)
閱讀全文 »

發表於 | 分類於

使用 SGD 做優化時, 如果 ill-conditioned of Hessian matrix, i.e. $\sigma_1/\sigma_n$ 最大最小的 eigenvalues 之比值, 會使得收斂效率不彰
(ref zig-zag).

可以想成 loss function 的曲面愈不像正圓則愈 ill-conditioned (愈扁平).

希望藉由 re-parameterization 來將 ill-conditioned 狀況降低.
一般來說 NN 的 layer 可以這麼寫:
$$y=\phi(w^Tx+b)$$ 把 weight vector $w$ 重新改寫如下:

$$w={g\over\|v\|}v\quad\quad(\star)$$ WN 就是將 $w$ 拆成用 unit vector $v/||v||$ 和 magnitude $g$ 兩個 variables 來表示

閱讀全文 »

發表於 | 分類於

由以前這篇文章知道, 對多顆不同 models 的結果取平均通常會得到更好的結果.
但如果對 models 的參數先取平均呢? 一樣會好嗎?
Stochastic Weight Averaging (SWA) 的這篇文章 “Averaging Weights Leads to Wider Optima and Better Generalization“ 嘗試說明這是有效的.
而實務上, PyTorch 和 PyTorch Lightning 也已經直接導入了 SWA 的 API. 甚至在語音辨識業界裡, 有取代 Kaldi 勢頭的 WeNet 裡面也有類似的機制.

本文直接截圖自己的 slides 內容, 而 Pdf 檔案可參考 這裡

投影片內容

直接上圖:

閱讀全文 »

發表於 | 分類於

Sharp V.S. Flat Local Minimum 的泛化能力

先簡單介紹這篇文章:
On large-batch training for deep learning: Generalization gap and sharp minima
考慮下圖兩個 minimum, 對於 training loss 來說其 losses 一樣.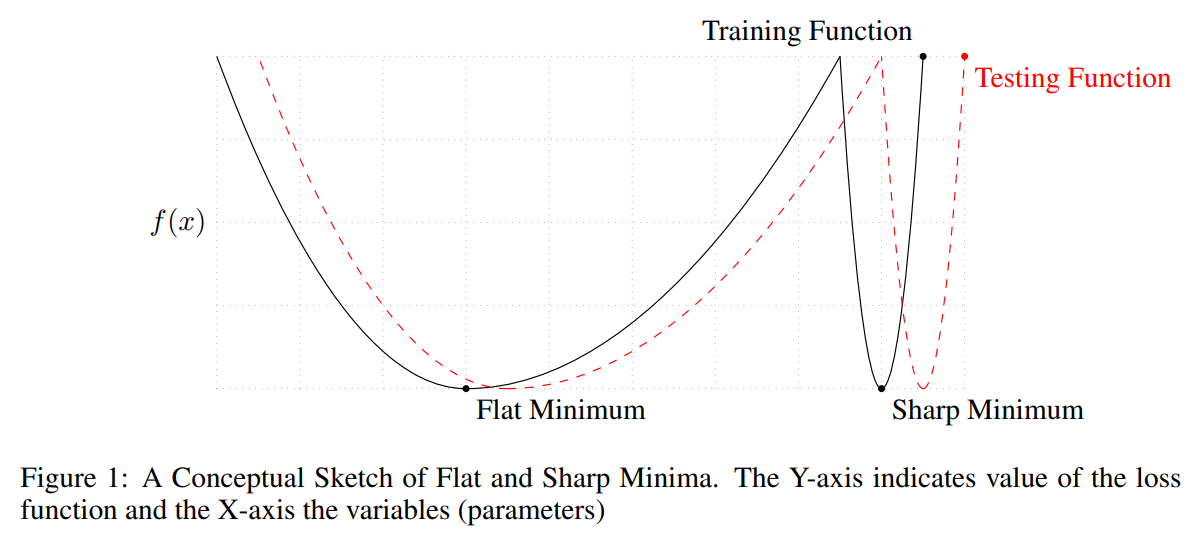
從圖可以容易理解到, 如果找到太 sharp 的點, 由於 test and train 的 mismatch, 會導致測試的時候 data 一點偏移就會對 model output 影響很大.
論文用實驗的方式, 去評量一個 local minimum 的 sharpness 程度, 簡單說利用 random perturb 到附近其他點, 然後看看該點 loss 變化的程度如何, 變化愈大, 代表該 local minimum 可能愈 sharp.
然後找兩個 local minimums, 一個估出來比較 sharp 另一個比較 flat. 接著對這兩點連成的線, 線上的參數值對應的 loss 劃出圖來, 長相如下: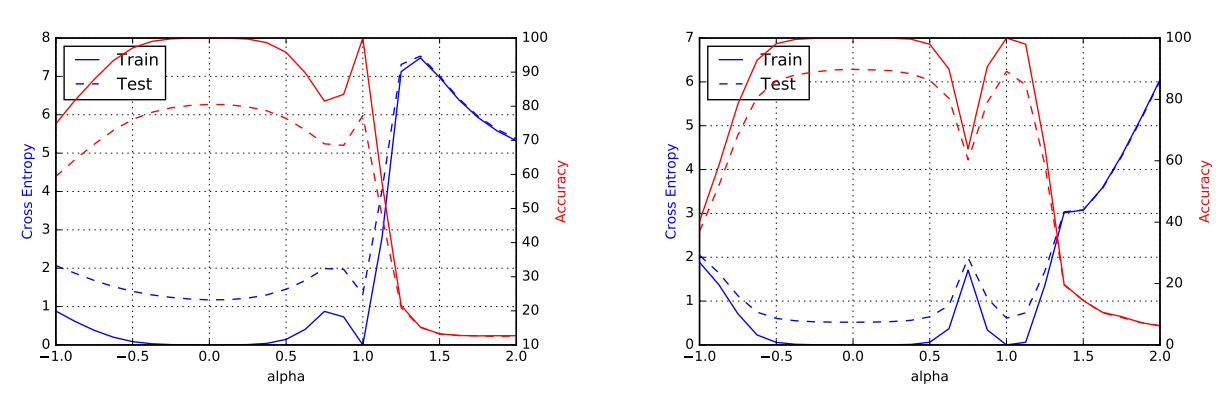
這也是目前一個普遍的認知: flat 的 local minimum 泛化能力較好.
所以可以想像, step size (learning rate) 如果愈大, 愈有可能跳出 sharp minimum.
而 batch size 愈小, 表示 gradient 因為 mini-batch 造成的 noise 愈大, 相當於愈有可能”亂跑”跑出 sharp minimum.
但這篇文章僅止於實驗性質上的驗證. Step size and batch size 對於泛化能力, 或是說對於找到比較 flat optimum 的機率會不會比較高? 兩者有什麼關聯呢?
DeepMind 的近期 (2021) 兩篇文章給出了很漂亮的理論分析.

閱讀全文 »

發表於 | 分類於

如果對於 Differential Equation 完全沒概念, 建議先看以下兩分鐘的影片
 - Solving Differential Equations vs. Solving Algebraic Equations
主要筆記了 Prof. Jeffrey Chasnov 在 Coursera 的兩門課 針對 numerical solution 解 ODE 的內容:
 1. Differential Equations for Engineers
 2. Numerical Methods for Engineers
本文介紹:
 1️⃣ Introduction to ODE: linear? ordinary? n-th order?
 2️⃣ Euler Method: 雖然簡單, 但 error 很大
 3️⃣ Modified Euler Method: error $O(\Delta t^3)$, 比 Euler method 小了一個 order
 4️⃣ Runge Kutta Methods: Modified Euler 方法是 Second-order RK 的一個特例
 5️⃣ Higher-order Runge-Kutta Methods: $n$-th order RK 的 error 為 $O(\Delta t^{n+1})$
 6️⃣ Higher-order ODEs and Systems: 以上都只介紹 first-order ODE 逼近法, 那 higher-order ODE 怎解?

👏 那兩門課的講義教授很佛心得都有附上:
Lecture notes: Differential Equations for Engineers
Lecture notes: Numerical Methods for Engineers

閱讀全文 »

發表於 | 分類於

先說我物理什麼的都還給老師了, 只能用自己理解的方式, 筆記下 Hamiltonian dynamic.

　💡 如果連我都能懂, 相信大家都能理解 HMC 了

但還是建議先看 MCMC by Gibbs and Metropolis-Hasting Sampling, 因為這篇要說的 Hamiltonian Monte Carlo (HMC) 是 Metropolis-Hastings (MH) 方法的一種, 只是 proposal distribution 從 random walk 改成使用 Hamiltonian dynamics 來做, 因而變的非常有效率 (accept rate 很高), 且對於高維度資料採樣也很有效.

首先粗體字如 $\mathbf{x}, \mathbf{v}, \mathbf{p}$ 都是 column vector, 而非粗體字表 scalar, e.g. $m,t$

閱讀全文 »

發表於 | 分類於

主要內容為這篇文章 “Generative Modeling by Estimating Gradients of the Data Distribution“

背景知識

Score-based generative modeling 的兩個核心概念:

  1. Score matching (SM):
    使用 score matching loss 讓 NN 直接學 score function: $\nabla_x\log p_{data}(x)$, 其中 $p_{data}(x)$ 為 data p.d.f.
    因此我們有一個 NN: $s_\theta(x)\approx \nabla_x\log p_{data}(x)$
    Score matching 在做什麼, 請參考系列文章:

  2. Langevin dynamics:
    Langevin dynamics 可以使用 score function, i.e. $\nabla_x\log p_{data}(x)$, 來取 sample, 取出來的 sample 具有 $p_{data}(x)$ 的分佈
    而我們已經用一個 NN $s_\theta(x)$ 來逼近 score function 了, 因此可以用 $s_\theta(x)$ 來取 sample, 步驟如下:
    給定一個固定的 step size $\epsilon>0$, initial value $z=\tilde{x}_0\sim\pi(x)$, 其中 $\pi(x)$ 是固定的 prior distribution, and $z_t\sim\mathcal{N}(0,I)$

    $$\tilde{x}_t = \tilde{x}_{t-1}+\frac{\epsilon}{2}\nabla_x\log p_{data}(\tilde{x}_{t-1})+\sqrt{\epsilon}z_t \\ \approx \tilde{x}_{t-1}+\frac{\epsilon}{2}s_\theta(\tilde{x}_{t-1})+\sqrt{\epsilon}z_t$$ 當 $\epsilon\rightarrow 0$, $T\rightarrow\infty$ 則 $\tilde{x}_T$ 等同於從 $p_{data}(x)$ 取樣!
    我們在這篇文章 忘記物理也要搞懂的 Hamiltonian Monte Carlo (HMC) 筆記
    非常仔細得解釋了為什麼可以這麼做, 注意到其實這裡涉及了很多知識, 依序包含 MCMC, Metropolis Hastings, Hamiltonian Dynamic, 最後才關聯到 Langevin Dynamics. 不過只想單純使用的話, 上面的描述就足夠.

藉由 Score Matching + Langevin Dynamics (SMLD), 我們發現如果成功學到 score function, 則可以從 random noise $z$ 產生符合 data distribution 的 sample.
而這正是 generative model 在做的事情, 此種方法論文稱為 SMLD
但是直接訓練出來的 SMLD 在真實資料上會有兩個問題導致做不好, 接著論文裡說明是什麼原因以及解決方法

閱讀全文 »

發表於 | 分類於

看了一些 score matching 的論文後, 就在網路上找了一下有沒有範例, 然後找到了這個 repo: [toy_gradlogp]
非常清晰易懂, 重點實作了:

  • Denoising Score Matching (DSM)
  • Deep Energy Estimator Networks (DEEN, 我怎麼覺得跟 DSM 等價?!)
  • Sliced Score Matching (SSM)
  • Sliced Score Matching with Variance Reduction (SSM-VR)
  • Langevin Dynamics (可以只根據 score function 取 sample)

雖然主要都是 PyTorch, 但 data pipeline 仍然使用 tensorflow
因此我就改寫了一下, 變成純 PyTorch, 並且也改成我習慣的資料夾結構和 config 使用 Hydra

改寫後的在這: [Score Matching Practicing in PyTorch]

以下接著說明兩個重點:

  1. Langevin Dynamics 簡介
  2. 怎麼把 gradient 也當成 loss?
閱讀全文 »

發表於 | 分類於

這是一篇論文筆記: “Sliced-Score-Matching-A-Scalable-Approach-to-Density-and-Score-Estimation”
建議看本文前請先參前兩篇: Score Matching 系列 (一) 和 Score Matching 系列 (二)

雖然 DSM (文章在系列二) 比起 SM 可以非常有效率的訓練, 但最多只能還原到 noisy 的分布, 且加噪的強度不易調整.
本篇 SSM or SSM-VR 則不會有此缺點, 且效果可以接近原來的 SM.

閱讀全文 »

發表於 | 分類於

這是一篇論文筆記: “A Connection Between Score Matching and Denoising Autoencoders”
建議看本文前請先參前一篇: Score Matching 系列 (一) Non-normalized 模型估計

前言

基於 Score Matching, 提出 Denoising Score Matching (DSM) 的目標函式, 好處是在 energy-based model 下:

  1. 不用將 score function 的 gradients 也納入 loss 去計算 (避免二次微分做 backprop 提高效率)
  2. 當 input $x$ 的維度很大也沒問題 (可以 scalable)

但缺點是:

  1. 最多只能學到加 noise 後的分布
  2. 加 noise 的 level 不好調整

這兩個缺點在下一篇 Sliced Score Matching (SSM) 可以得到改善
這篇論文最後也點出了 denoising autoencoder 跟 score matching 的關係 (實際上就是 DSM loss)

以下正文開始

閱讀全文 »