在這篇之前的 NAS (Neural Architecture Search) 主流方法為 evolution or RL 在 discrete space 上搜尋, 雖然可以得到當時最佳的結果, 但搜索的 cost 很高.
這篇提出 DARTS (Differentiable ARchiTecture Search) 將 NAS 變成 continuous relaxation 的問題後, 就能套用 gradient-based optimize 方法來做 NAS. 因此比傳統方法快上一個 order. 雖然 gradient-based NAS 在這篇文章之前就有, 但是之前的方法沒辦法像 DARTS 一樣能套在各種不同的 architecture 上, 簡單講就是不夠 generalized.
核心想法是, 如果一個 layer 能包含多個 OPs (operations), 然後有個方法能找出最佳的 OP 應該是那些, 對每一層 layers 都這樣找我們就完成 NAS 了.
圖片來源, 或參考這個 Youtube 解說, 很清楚易懂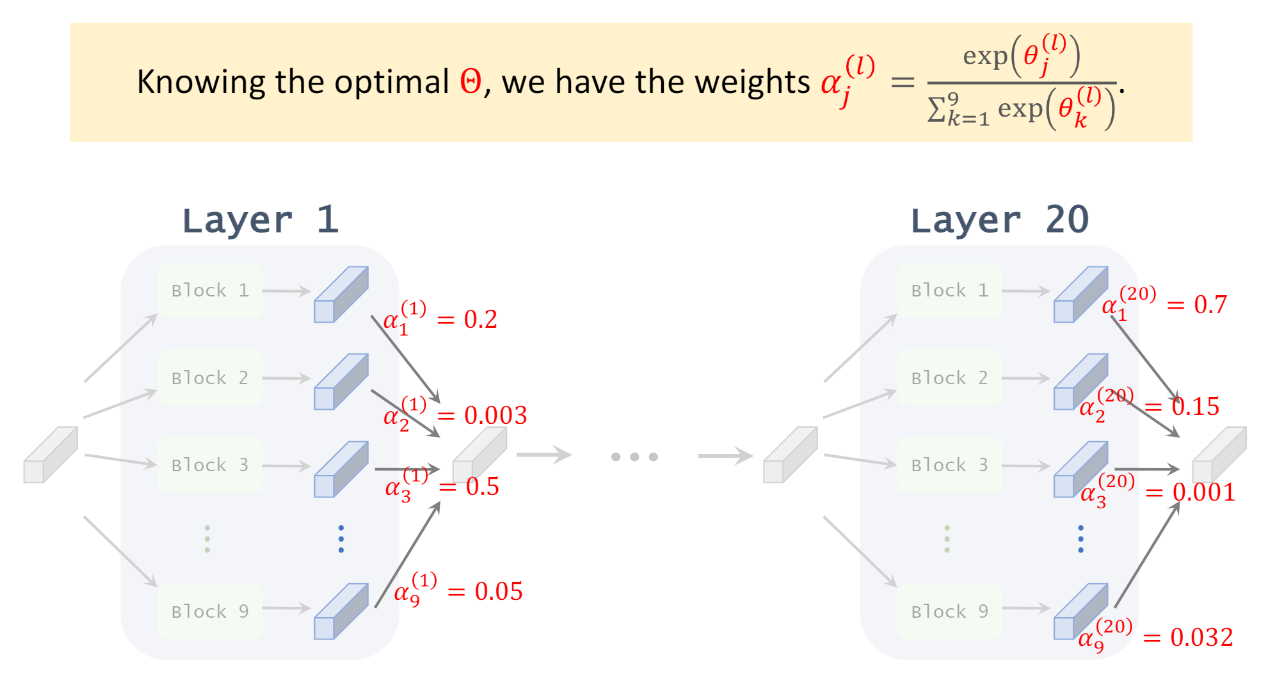 不過關鍵是怎麼找? 這樣聽起來似乎需要為每個 OPs 都配上對應可訓練的權重, 最後選擇權重大的那些 OPs? 以及怎麼訓練這些架構權重?
不過關鍵是怎麼找? 這樣聽起來似乎需要為每個 OPs 都配上對應可訓練的權重, 最後選擇權重大的那些 OPs? 以及怎麼訓練這些架構權重?
或這麼類比: 直接訓練一個很大的 super network, 根據 OP 對應的架構權重來選擇哪些 OPs 要留下來, 大概類似 model pruning 的想法
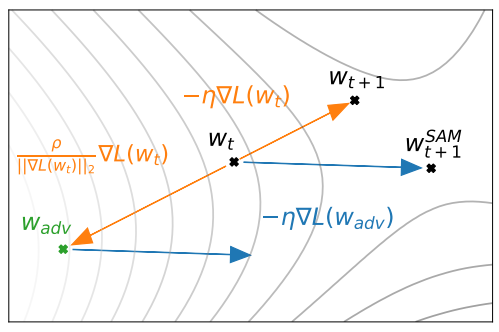 目前的 weight $w_t$ 的 gradient step 為
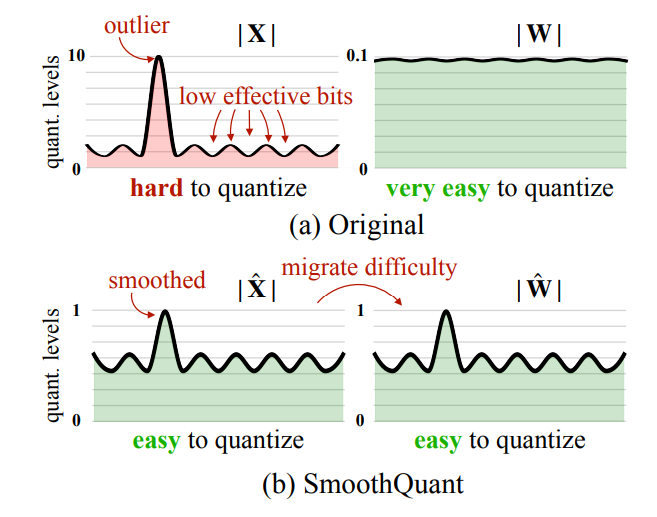
目前的 weight $w_t$ 的 gradient step 為 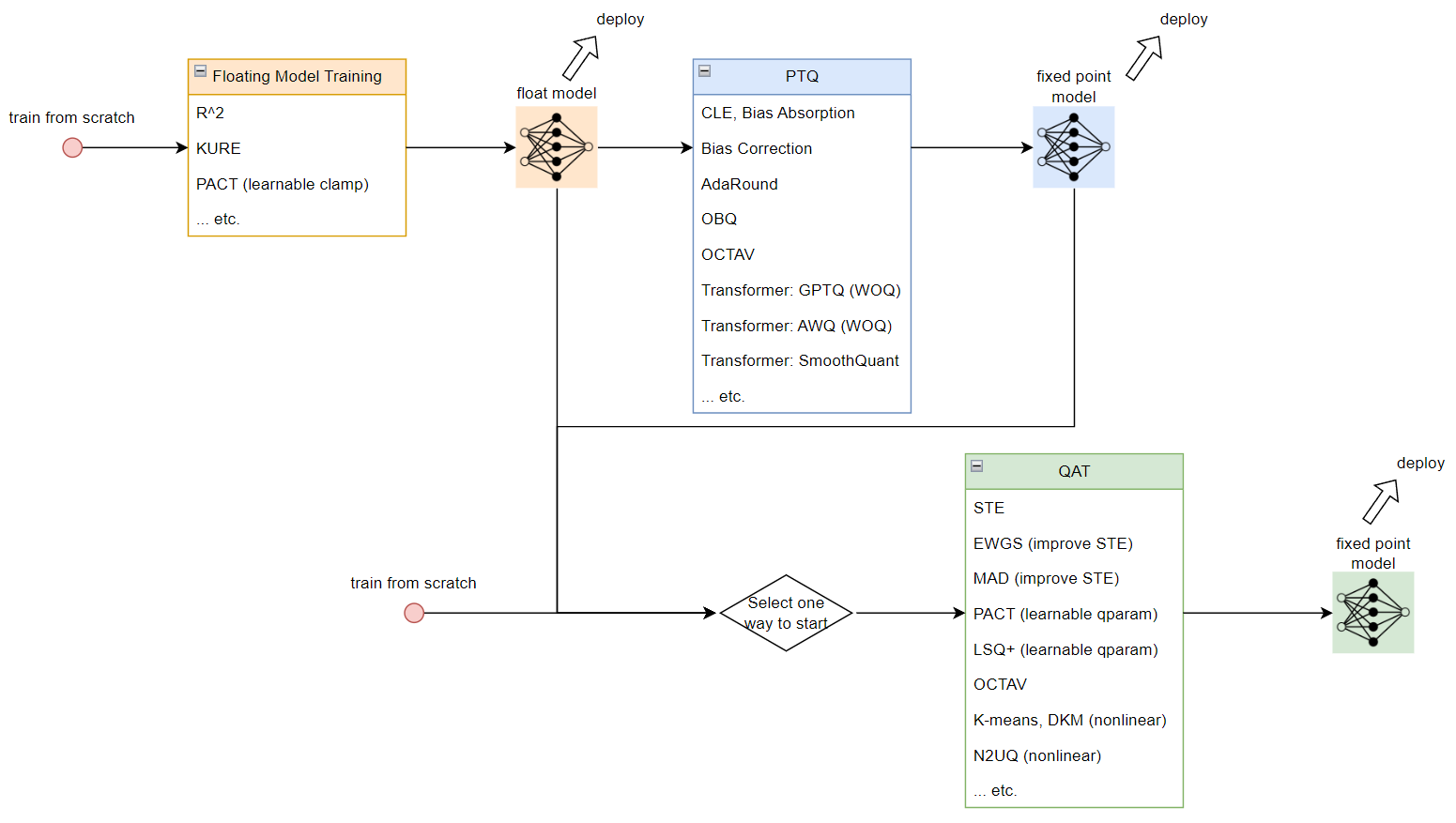 Post Training Quantization (PTQ) 稱事後量化. Quantization Aware Training (QAT) 表示訓練時考慮量化造成的損失來做訓練
Post Training Quantization (PTQ) 稱事後量化. Quantization Aware Training (QAT) 表示訓練時考慮量化造成的損失來做訓練
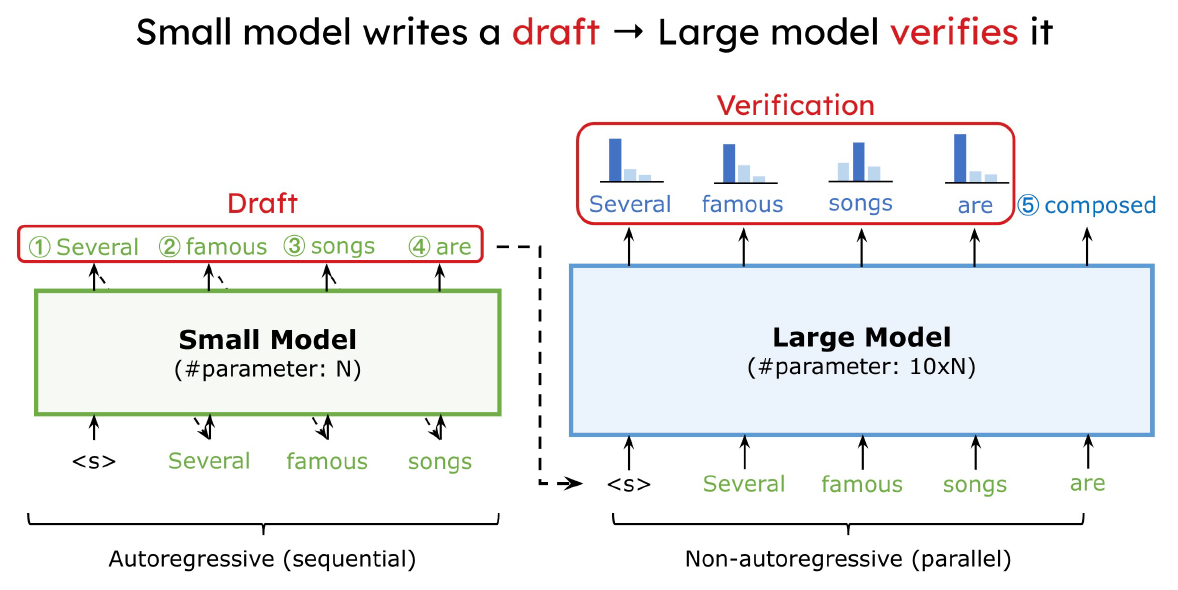 利用 small model 先提出一些 draft tokens, 然後用 large model 來驗證. 如果大部分都接受, 直覺上可以省去很多 large model 的呼叫次數, 因此加速. 方法十分簡單, 不過其實魔鬼藏在細節裡, 跟原本只使用 large model 的方法比較有幾個問題要回答:
利用 small model 先提出一些 draft tokens, 然後用 large model 來驗證. 如果大部分都接受, 直覺上可以省去很多 large model 的呼叫次數, 因此加速. 方法十分簡單, 不過其實魔鬼藏在細節裡, 跟原本只使用 large model 的方法比較有幾個問題要回答: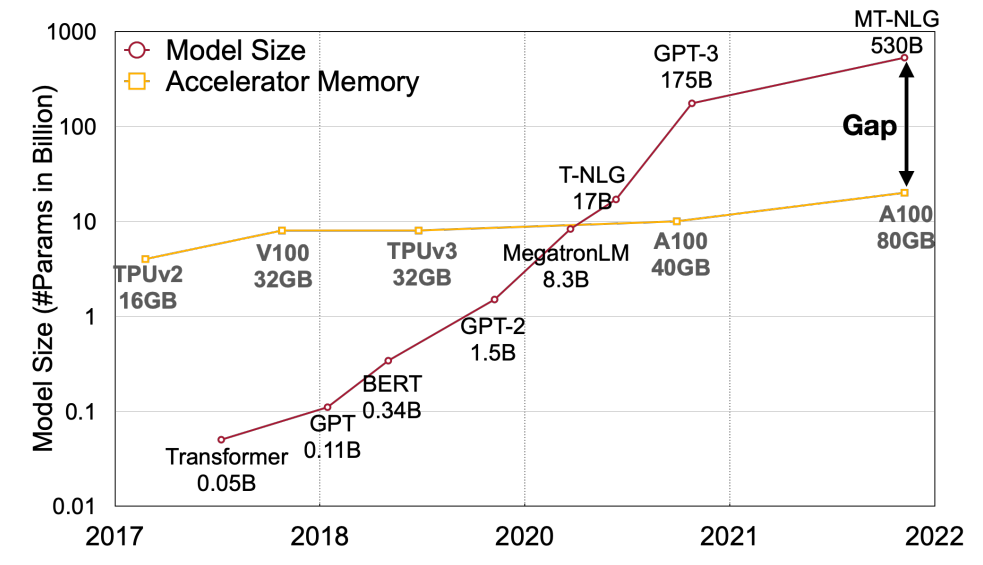 如何降低 memory 使用量將變的很關鍵, 因此 Activation-aware Weight Quantization (AWQ) 這篇文章就專注在 Weight Only Quantization (WOQ), 顧名思義就是 weight 使用 integer 4/3 bits, activations 仍維持 FP16.
如何降低 memory 使用量將變的很關鍵, 因此 Activation-aware Weight Quantization (AWQ) 這篇文章就專注在 Weight Only Quantization (WOQ), 顧名思義就是 weight 使用 integer 4/3 bits, activations 仍維持 FP16.